부동산 과소거래시장의 하위시장 가격지수 작성을 위한 계층 모형의 활용 방안
Abstract
The scale of investment in the real estate market in Korea continues to grow every year, and accordingly, the demand for market information for diagnosing market conditions and making investment decisions increases. Unlike the housing market, commercial real estate market has an exclusive information system that lacks information available to investors. In particular, it is not easy to estimate a stable index, even if various information is available for the office market, with a low frequency of transactions. Various attempts have been made to estimate the index in Korea, but there is a limit to showing more detailed sub-market information.
Therefore, this study estimated the price index based on the transaction-based data of the office sub-market with a low transaction frequency. A model combining a hierarchical structure with a repeat-sales model was used, and various indicators such as statistical reliability, stability, index revision, and predictive performance of the model were compared. It was confirmed that the index estimation performance was improved, and it is expected that the performance will be better, especially in situations where transactions are less frequent. In addition, the possibility of expanding and utilizing the research model was suggested by estimating the subdivided regional indices instead of the district, by utilizing the advantage of flexible model modification.
Keywords:
Thin Market, Office Price Index, Transaction-Based Data, Hierarchical Model, Real Estate Sub-Market키워드:
과소거래시장, 오피스 가격지수, 실거래 자료, 계층 모형, 부동산 하위시장Ⅰ. 서 론
부동산 가격지수는 부동산 시장의 가격 움직임을 대표적으로 나타내어주는 지표로서 부동산 시장의 위험과 수익성 등 시장 상황을 직접적으로 보여준다. 따라서 시장의 투자자 및 소비자에게도 수익률과 변동성에 관한 정보를 제공함으로써 투자 성과를 평가하고 투자 여부에 대한 의사결정을 할 수 있도록 지원하는 역할을 한다. 또한 정부의 부동산 규제 강화 및 완화 결정, 통화정책 수립 방향 등 정책적 의사결정을 도울 수 있다. 이외에도 수익률 측정에 기초가 되는 부동산 가치 평가 시 시점 보정에 활용되며(송영선 외, 2021), 파생상품으로 활용할 수 있다(Deng and Quigley, 2008; 류강민 외, 2011). 이와 같이 부동산 가격지수의 역할이 크기 때문에 해외를 중심으로 상당히 오랜 기간 동안 정확한 가격지수 산정을 위한 노력들이 이루어졌다.
한편, 보다 세분화 된 부동산 가격지수는 공간 및 자산시장을 더 잘 표현(Francke and van de Minne, 2017)하여 많은 정보를 보여주기 때문에 활용성 측면에서 유용성을 가진다(van de Minne et al., 2020). 특히 시장의 위험 분산을 위한 포트폴리오 최적화에 유용하게 활용될 수 있다(홍자영·이용만, 2003; 박치형, 2012). 조금 더 큰 틀에서는 시장 정보의 투명성과 정보 비대칭 해소라는 측면에서도 필요하다(송영선 외, 2021). 그러나 거래자료가 충분하지 않은 과소거래시장(thin market)은 안정적인 가격지수 산정에 어려움이 있다. 아파트 시장은 광역 단위로 볼 때는 거래량이 많더라도 지역 범위를 세분화할수록 그 수는 점차 감소하며, 특히 전국적인 거래량 자체가 적은 상업용부동산과 같은 유형은 이러한 문제가 더욱 확대되어 나타난다.
이러한 한계를 해결하기 위한 다양한 연구들이 선행되었으나 실무적으로 국내 실정은 세분화된 가격지수에 대한 요구를 잘 따라가지 못하고 있는 상황이다. 실거래가 지수에 한정하면, 한국부동산원의 실거래가격지수는 공동주택에 대해서만 매매 및 전세 가격지수를 공표하고 있으며, 시도별 및 서울시 5대 생활권역별로만 지수가 작성되고 있는 한계가 있다1). 비주택 유형에 대해서는 최근 공표를 시작한 국민은행 오피스 가격지수2)를 제외하면 과거에 소수의 민간업체에서 오피스 매매가격지수를 공표했던 몇 건의 사례가 전부이며 그마저도 중단된 상태이다.
따라서 본 연구에서는 과소거래시장에서의 세분화된 하위시장 지수를 산정하는 방법론을 검토하고 제안하고자 한다. 이를 위해 다음과 같은 세 가지 연구 모형을 결합하여 활용하였다. 먼저, 실거래 자료를 이용하여 가격지수를 산정할 때 크게 헤도닉 모형(Lancaster, 1966; Rosen, 1974)과 반복매매 모형(Bailey et al., 1963)의 두 가지 형태의 모형을 이용할 수 있는데 이 둘은 서로 상반되는 장·단점을 가지고 있다. 그러나, 무엇보다도 반복매매 모형은 도시공간구조 변화에 따른 부동산의 입지가 가지는 가치의 변화를 지수에 담아낼 수 있고(이창무 외, 2007), 각 부동산의 매수와 매도 사이의 가격변화율을 기반으로 하고 있어 투자자들의 직접적인 경험을 반영할 수 있다는 이점(Geltner et al., 2014, p.658)이 있기 때문에 반복매매모형을 기본 모형으로 이용하였다. 두 번째로 확률적 구조를 가정한 시계열 모형을 이용하였다. 이를 이용하게 되면 실제보다 지수가 평활화될 가능성이 있지만, 정확도가 향상되고, 과소거래시장에서 잘 작동한다는 장점이 있다(Schwann, 1998; Francke, 2010; 송영선 외, 2021). 마지막으로 상·하위 시장 간 계층적(hierarchical) 구조를 가정한 계층 모형을 이용하였다. 부동산 시장은 크게 공간과 자본시장으로 나누어질 수 있는데, 개별 자산이나 특정 하위시장의 특이한 가격 움직임은 공간시장을 반영하고 있다. 그러나 시간의 흐름에 따른 할인율의 변화에서 야기된 자본의 기회비용 변화는 자산의 가격 변동성을 만들어내며(van de Minne et al., 2020), 이로 인해 서로 다른 공간시장 간에도 자본시장에 기반한 가격 움직임을 공통적으로 가지게 된다(Geltner et al., 2014, p.556). 따라서 하나의 범주로 묶일 수 있는 하위시장들의 공통적인 가격변동 추세를 공유한다는 개념을 기초로 계층적 구조를 가정할 수 있다. 이러한 가정에 기초하여 지수를 산정하면 각각의 하위시장의 지수를 산정하기 위해 다른 모든 시장의 가격변동 정보를 모두 이용하며 각각의 정보를 효과적으로 공유하여 효율적인 추정이 가능해진다.
본 연구는 다음과 같이 구성되어 있다. Ⅱ장에서는 관련 선행연구를 고찰하고 본 연구에서 활용할 방법론을 선택한 후, Ⅲ장에서 연구 구성과 자료, 지수 추정 방법을 소개하였다. 이를 바탕으로 이후에는 크게 두 가지 방향으로 연구를 진행하였다. 먼저, Ⅳ장의 1절에서는 최소한의 거래자료 확보가 가능하면서도 거래 빈도가 적어 안정적인 지수 산정에 어려움이 있는 국내 오피스 시장을 대상으로 하여 권역별 가격지수를 산정하였으며, 2절에서는 추가적인 모형의 설정을 통해 보다 세분화된 세부 지역별 지수를 추정하였다. 이때 각각의 지수 산정 결과에 대한 평가를 위해 지표를 통해 모형의 추정성능을 평가하였다. 이후 Ⅴ장에서는 연구 결과를 요약하고 시사점을 제시하였다.
Ⅱ. 선행연구 고찰
1. 선행연구 검토
부동산 과소거래시장에 대한 신뢰할 수 있는 가격지수 산정은 오랫동안 가격지수 연구 분야에서 큰 과제였다. 과소거래시장의 가격지수 산정에 어려움이 있는 것은 부동산의 이질적인 특성을 적절하게 통제하기 어려운 탓도 있을 것이다. 그러나 Schwann (1998)은 근본적인 원인으로 시점별로 이용 가능한 거래 자료가 부족하여 발생하는 자유도 확보의 문제를 지적하였으며, 실제로 다수의 관련 연구들이 자유도 문제를 해결하는 방향으로의 개선 방안들을 제시해왔다.
자유도 문제를 해결하는 가장 간편하고 직접적인 방법 중 하나는 자료의 집합을 늘리는 것이다. 송영선 외(2020)은 인접한 2, 3개월의 자료를 병합하여 동일 시점의 자료로 가정하는 과정을 반복하여 전체 자료 집합을 늘리는 자료 중첩 방식(rolling method)으로 반복매매 지수를 산정하였다. 이러한 방식은 Shimizu et al.(2010)과 Hill et al.(2022)의 연구에서도 헤도닉 가격지수를 산정하는 데 이용되었다. 이러한 방식의 활용은 자료 수를 늘려 자유도를 확보할 뿐만 아니라 인접한 시점 간에 독립적이지 않은 구조를 만들어내어 지수의 신뢰도를 개선하는 데 효과적으로 작동하는 것으로 확인되었다. 그러나 이는 반대로 지수에 시차를 발생시키는 문제를 안고 있으며, 시간더미 변수를 추정하는 모형을 그대로 이용할 때 거래가 발생하지 않은 시점이 적지 않게 존재한다면 여전히 완전한 지수 산정이 불가능한 한계가 있다.
자유도 문제를 개선하는 또 하나의 방법은 지수의 작성 주기를 길게 설정하는 것이다. 그러나 지수의 주기가 길면 지수의 활용성이 떨어질 수 있는데, Bokhari and Geltner(2012)는 MIT 부동산 연구센터에서 개발한 긴 주기를 짧은 주기로 변환하는 2단계 추정법을 소개하고 있다. 이는 구체적으로 한 개 분기씩 시차를 둔 연 지수 4개를 먼저 추정한 후, Moore-Penrose의 의사역행렬을 통해 분기 단위의 지수를 계산하는 방식이다. 최종적으로 산출되는 것은 분기 지수이지만, 연 지수를 기초로 하기 때문에 지수의 통계적 신뢰도와 안정성이 향상되는 결과를 얻을 수 있다. 이는 이후에도 다양한 지수 산정 연구에 활용되었다(Chegut et al., 2013; Bourassa and Hoesli, 2017; 황규완·손재영, 2017; 류강민·송기욱, 2020). 그러나 이 또한 자료 집합을 늘리는 방식과 마찬가지로 인접 시점의 자료가 포함된 지수의 변동률이 활용되기 때문에 지수에 시차가 발생하는 한계를 가지고 있다.
이외에도 시간효과 모수를 함수형태로 설정하여 지수를 산정한 연구들도 이루어졌다. McMillen and Dombrow(2001)와 McMillen and McDonald(2004)는 푸리에 변환을 통해 모수의 수를 줄여서 지수를 추정하기도 하였다. 또한 3개의 멱법칙(triple power law)으로 생성한 가상의 분포로부터 중위수 지수를 추정하는 Radar Logic사의 방법론을 활용하는(류강민 외, 2017) 등의 다양한 방식들로 과소거래시장에서 효율적인 지수 추정이 가능한 대안들이 제시되었다. 그러나 이와 같은 방법들은 지수의 초기 시점이 불안정하다는 공통적인 문제를 안고 있다.
자유도 문제를 개선하기 위한 다양한 방안들 중에서도 가장 적극적으로 이용된 것은 가격지수 모수에 시계열 구조를 도입한 것이다. Schwann(1998)은 자기회귀과정을 도입한 시계열 구조에 기초하여 상태공간 모형을 설정하고 이를 바탕으로 헤도닉 가격지수를 산정하였다. 특히 지수의 표준오차, 신뢰구간 등을 비교하여 연구 모형이 기존의 방법론에 비해 지수의 정확도를 높일 수 있다는 점을 확인하였다. 이러한 방법론은 국내에서 박헌수(2007)를 통해 서울시 강남구 아파트 가격지수 산정에 적용되기도 하였다. Goeztmann(1992)은 랜덤워크 과정(random walk process)을 시간효과에 도입하였으며, ordinary least squares(OLS), generalized least squares(GLS), 3단계 weighted repeat sales(WRS), James and Stein, 베이즈(bayes) 등 다양한 추정 방식을 비교하였다. 여기에서 제안된 랜덤워크 과정을 도입한 지수 산정 모형은 Francke(2010)의 연구를 통해 일반화한 국지선형추세(local linear trend, LLT) 모형으로 발전되었다. 국지선형추세 모형을 기반으로 한 연구 결과에서는 베이지안 추정을 활용하여 표본이 적은 경우에도 변동성과 표준편차가 작은 지수의 산정이 가능하다는 점이 확인되었다. 국지선형추세 모형은 모수에 대한 가정에 따라 랜덤워크(random walk, RW) 모형, 추세항을 포함하는 랜덤워크(random walk with drift, RWD) 모형으로 형태 변형이 가능한데, 이상의 세 가지 구조적 시계열 모형(structural time series model)은 국내의 시장을 대상으로도 활용된 바 있다. 차승호(2020)는 세 가지 구조적 시계열 모형을 이용하여 전주시 토지 실거래가 지수를 산정하여 지수의 통계적 신뢰도가 높고 안정적인 지수 산정이 가능함을 확인하였으나 지수 작성 기간이 4년에 불과하여 면밀한 검토에는 한계가 있었다. 송영선 외(2021)는 서울시 오피스 가격지수를 산정하는데 세 가지 모형(RW, RWD, LLT)을 활용하였다. 이는 기본적인 반복매매 모형, 자료 중첩 방식, MIT 2단계 추정법을 이용한 결과와 비교하여 지수의 통계적 신뢰도, 안정성, 지수 변화(index revision) 등 다양한 측면에서 모두 지수 추정성능이 우수한 것으로 나타났다. 이상의 시계열 구조를 활용한 지수 모형들은 공통적으로 통계적인 신뢰도가 높고 앞서 소개한 방법론들과 달리 지수에 시차가 두드러지게 나타나지 않는다는 점에서 이점을 가지고 있는 것으로 나타났다. 그러나 지수가 과하게 평활화될 가능성이 있으며 이로 인해 시장 가격 움직임의 방향이 변화하는 전환점(turning point)을 제대로 포착하지 못할 가능성이 있다는 지적이 있다.
한편, 하위시장 가격지수 산정에 특화된 방법론에 대한 연구들도 이루어졌다. 이들은 하위시장의 가격지수 산정을 위해 상위시장의 가격 움직임에 대한 정보를 이용하는 방식으로 지수 모형을 구성하였다. 첫 번째는 계층 모형을 활용한 것이다. Francke and Vos(2004)는 지역과 주택 유형별 계층 구조를 도입하여 네덜란드의 헤도닉 주택가격지수를 추정하였고, Francke and van de Minne(2017)은 미국과 네덜란드의 주거 및 상업용부동산 시장의 반복매매 지수 산정을 위해 하위시장을 나누는 두 군집(지역, 부동산 유형)을 병렬적으로 연결한 계층적 구조를 도입하였다. 이들 연구의 결과에서 공통적으로 계층 모형의 활용으로 신뢰도가 높은 지수 산정이 가능하다는 점을 확인하였고, 특히 거래 자료 수가 적을수록 더욱 잘 작동한다는 점을 확인하였다.
국내 연구 중에서는 권민성 외(2022)의 연구에서 Francke and van de Minne(2017)의 계층적 반복매매 모형이 이용되어 서울시 아파트 실거래가 지수를 산정하고 이를 바탕으로 다시 시세를 만들어내었다. 서울시 아파트 시장은 거래 자료가 충분히 확보되기 때문에 전체로 보면 과소거래시장이 아니지만, 거래 자료가 적은 아파트 단지별 지수를 산정하여 평활화 및 시차 등의 한계가 있는 기존의 시세 조사 기반 가격지수를 대체할 수 있음을 확인하였다.
van de Minne et al.(2020)은 계층 모형이 아니라 하위시장들의 집합인 상위시장의 가격지수를 하위시장 가격지수 산정 모형에 설명변수로 포함시키는 방식으로 상위시장 정보를 활용하여 미국의 부동산 하위시장 가격지수를 산정하였다. 이 논문에서는 Francke(2010)의 구조적 시계열 모형과 달리 1차 자기회귀과정을 가정하였으며, 상위시장 가격지수를 설명변수로 하는 모수를 함께 모형에 담아냄으로써 기존의 방법론과 비교하여 신뢰도가 더 높고 강건한 가격지수를 산정할 수 있음을 보였다. 특히, 이 논문은 지수 변화의 메커니즘과 이를 줄이는 방법에 집중하고 있는데, 새로 제안한 모형으로 산정된 지수에서 지수 변화가 큰 폭으로 줄어든다는 점을 확인하였다.
2. 선행연구의 종합
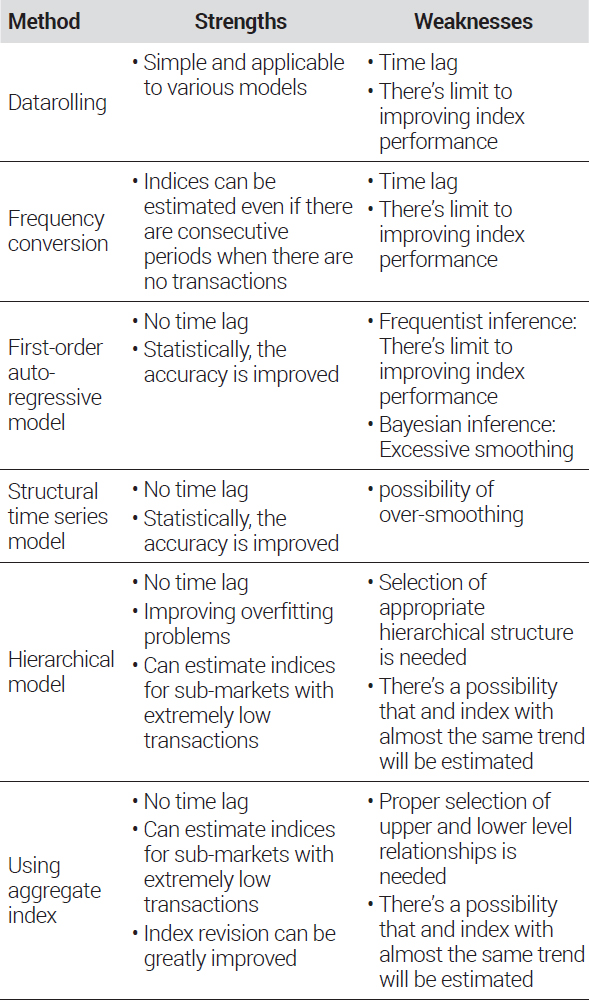
이상의 선행연구 검토 결과들을 종합할 때 각 방법론들의 특징은 <표 1>과 같다. 먼저, 자료 중첩 및 지수의 주기 변환 방식은 활용 자유도가 높고 일정 부분 지수의 안정성 등 통계적 신뢰도 개선이 가능한 장점이 있다. 그러나 기본으로 활용하는 모형에 한계가 크다면 이들 방법론 역시도 극단적인 상황에서는 여전히 한계를 가질 수밖에 없다. 또한 무엇보다도 지수에 1~2개 분기 가량의 시차가 공통적으로 발생하는데 이는 지수의 적시성 및 활용성 측면에서 치명적인 약점으로 작용할 것이다.
이에 비하면 시계열 함수를 이용한 방법론들은 더욱 정확한 지수 추정이 가능한 것으로 나타났다. 특히 시계열 함수 내 인접 시점 간의 연결고리는 추가적인 정보의 활용으로 거래 자료가 부족한 상황에서도 안정적인 지수 산정을 가능하게 하는 것으로 나타났다. 그러나 1차 자기회귀 모형으로 지수를 산정할 때 극단적으로 거래 자료가 부족한 상황에서는 여전히 약점들이 확인되었다. 빈도주의 추정에 기초한 상태공간 모형을 활용할 경우에는 여전히 안정적인 지수 산정에 한계가 확인되었으며, 베이지안 추정에 기초한 지수 추정 시에는 오히려 과하게 평활화가 이루어지는 것을 확인하였다. 구조적 시계열 모형 중 LLT 모형도 베이지안 추정을 활용한 1차 자기회귀모형과 같이 과하게 평활화가 이루어지는 단점이 존재하는 것으로 나타났다. 이러한 경우에 2008년 금융위기 이후의 상황과 같이 가격 움직임의 방향이 변화하는 전환점을 잘 포착하지 못하게 되는데, 이 또한 지수의 중요한 역할을 다하지 못하는 상황에 놓이게 되는 치명적인 문제점 중 하나이다.
계층 모형과 상위지수를 설명변수로 활용하는 방식의 하위시장 지수 산정 방법론들은 시계열 함수를 이용한 방법론들이 가지는 한계점들을 일정 부분 보완하는 역할을 한다고 볼 수 있다. 특히 하위시장에 거래가 발생하지 않더라도 상위시장에 거래가 발생하였다면 지수 산정이 가능하다. 또한 계층 모형의 경우에는 계층적 구조를 도입함으로써 과적합 문제를 개선할 수 있으며, 상위지수 활용 방식의 경우에는 반복매매 모형이 가지는 지수 변화의 문제를 큰 폭으로 개선할 수 있는 이점들이 확인되었다. 그러나 이들 모두 시장의 상·하위 관계에 대한 가정이 적절하게 이루어지지 못한다면 역시나 편의가 발생할 가능성을 가지고 있다.
본 연구에서는 이상의 선행연구 검토 과정을 통해 서울시 오피스 하위시장 가격지수 산정에 이용할 모형으로 계층 모형을 선택하였다. 계층 모형을 이용하면 다양한 이점들을 기대할 수 있다.
첫 번째는 계층 모형의 특성에 의한 것인데, 계층 모형에서는 상·하위 수준의 모수들이 상호 간에 영향을 미치는 구조적 의존성을 가지게 되어(Kruschke, 2018, 최정렬 역, p.236), 이로 인해 모수 추정 시 수축(shrinkage)이 발생한다. 수축은 상위 수준 모수에 가까운 방향으로 하위 수준의 모수가 이동하여 나타나는 것으로 이러한 특성은 표본의 잡음에 영향을 보다 적게 받는 추정치를 얻어내는데 이점을 가져다준다. 따라서 계층 모형을 이용함으로써 자료 수가 부족한 상황에서 나타날 수 있는 과적합(overfitting) 문제의 개선을 기대할 수 있다(McElreath, 2020, p.414).
두 번째는 주어진 자료를 모두 이용함으로써 효율적인 하위시장 지수 추정이 가능하다는 점이다. 이러한 이점은 극단적으로 자료가 부족한 하위시장 지수를 산정할 때 더욱 효과를 발휘할 수 있는데, 최근 시점에 거래가 발생하지 않아 지수가 중간에 끊길 수밖에 없는 상황에서도 상위시장에 거래가 존재한다면 상위시장 추세를 기반으로 하여 하위시장 지수 산정이 가능하다(Francke and van de Minne, 2017).
다만, 계층 모형은 하위시장 지수 산정을 위한 계층적 구조의 활용을 가능하게 해주는 것일 뿐이며 기본적으로 지수 산정을 위한 모형의 선택이 선행되어야 한다. 따라서 선행연구 검토 결과를 바탕으로 구조적 시계열 모형을 지수 산정을 위한 기초 모형으로 활용하였다. LLT 모형의 경우에는 앞서 논의한 것과 같이 과하게 평활화될 위험이 존재하지만, 특정 모수에 대한 적절한 제약을 통해 전환점 식별이 가능하도록 변형이 가능하며, 송영선 외(2021)의 연구를 통해 서울시 오피스 시장에 적용할 수 있는 가능성을 이미 확인한 바 있다.
3. 연구의 차별성
본 연구는 다음과 같은 두 가지 측면에서 차별성을 지닌다. 먼저, 계층 모형을 한국의 과소거래시장에 적용하여 나타나는 특성을 확인하고, 기존 방법론을 비교하여 계층 모형의 이점을 밝혀 안정적인 오피스 하위시장 지수를 산정하는 방안을 제시한다. 이는 국내에서 그간 이루어지지 못한 새로운 시도이다. 두 번째, 기존 연구에서는 한 가지 형태의 모형만을 제시하거나 동일한 틀 내에서 모형의 변형에 따라 나타나는 차이를 비교하였다면, 본 연구에서는 기본적인 형태의 모형에 더하여 시장 특성을 고려한 추가적인 지수 산정 모형을 제시한다. 이때 본 연구에서 제안하는 모형은 추후 관련 연구에서 연구자의 논리에 따라 유연하게 변형하여 활용할 수 있다는 점에서 단순히 본 연구에서 제시하는 것에 그치지 않고 다양한 활용 가능성을 제시한다.
Ⅲ. 분석의 틀
1. 분석 개요
본 연구의 실증분석은 크게 2단계로 구분된다. 첫 번째는 앞서 논의된 계층 모형을 기초로 하여 서울시 오피스 시장의 권역별 하위 지수를 산정하고, 통계적 신뢰도, 지수 안정성, 지수 변화(index revision) 등의 측면에서 계층 구조를 적용하지 않은 개별 추정모형과 비교한다. 두 번째로는 첫 번째에서 산정한 권역을 보다 세분화하여 10개의 지역별 하위 지수를 산정한다. 이때, 세분화된 지역별 지수는 하위시장의 특성을 고려하여 하나의 계층 구조를 추가로 도입한 연구 모형을 활용한다.
한편, 권역별 지수를 산정할 수 있다 하더라도 오피스 빌딩이 밀집된 핵심적인 지역과 그 외 지역 간에 차이가 있을 수 있으며, 서로 다른 입지의 거래 자료들이 섞여 있는 한계가 있다. 따라서 이를 보다 세분화하여 지표를 작성한다면 보다 상세한 시장 정보를 제공할 수 있을 것이다.
2. 분석 대상
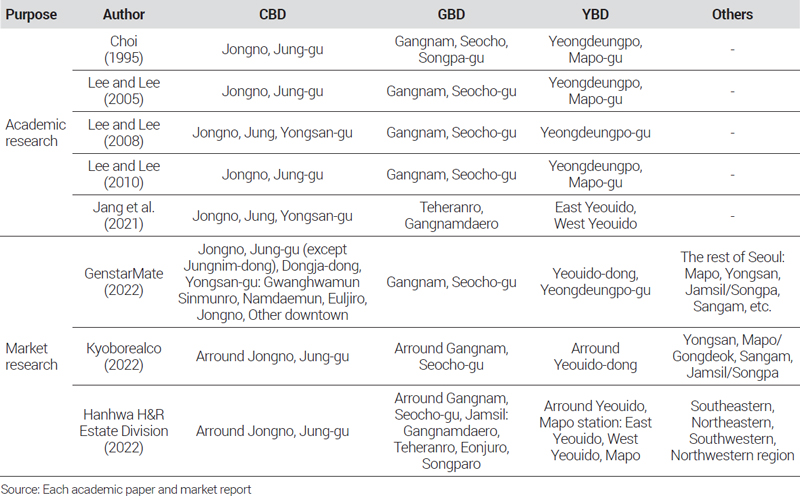
본 연구는 2000년 1분기부터 2022년 2분기까지 서울시에서 거래된 오피스 거래 자료를 바탕으로 지역에 따라 구분한 하위시장 가격지수를 산정한다. 이를 위해서는 먼저 오피스 빌딩이 무엇인가에 대한 기준 설정이 필요하다. 오피스 시장과 관련된 연구들 중 오피스 빌딩에 대한 사전적 정의3)를 담고 있는 연구들은 일부 존재하지만(허진호, 1998; 정유신, 2010), 실증분석의 기초가 되는 자료 수집을 위한 구체적인 기준에 대해서는 명확하게 합의가 되어있지 않은 상황이다. 다만, 학술연구 및 마켓리포트 등에서 오피스 빌딩의 기준을 제시한 사례(표 2)를 참고하여 본 연구에서는 건축물 연면적이 3,300m2 이상이고 지상 층수가 5층 이상인 건축물 중 건축물대장의 층별개요를 통해 계산된 오피스 용도 면적의 전체 연면적 대비 비율이 50% 이상인 건축물을 오피스 빌딩으로 기준 삼아 자료를 수집하였다.
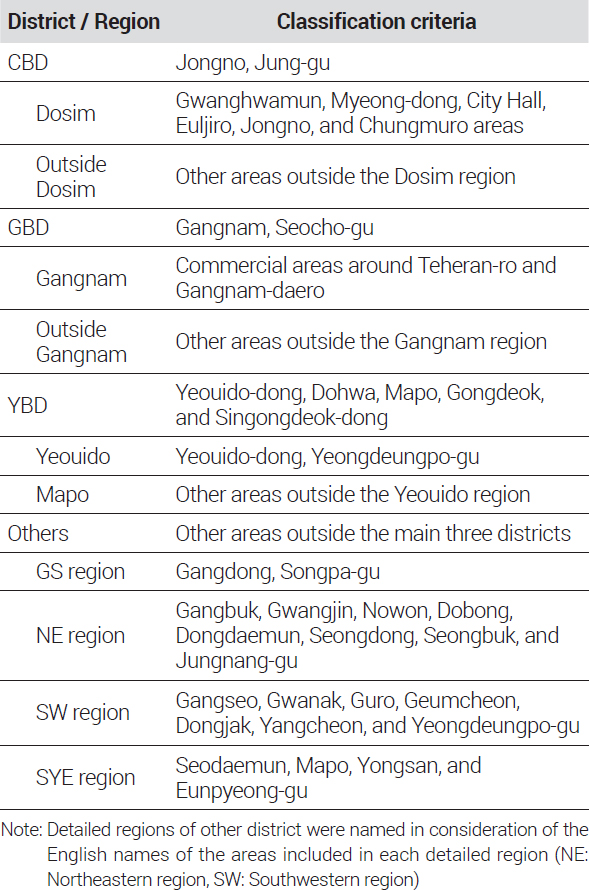
또한 본 연구의 주요 목적이 하위시장 가격지수를 산정하는 것이기 때문에 하위시장을 구분하는 것 또한 중요하다. 하위시장을 나눌 때 입지적 근접성과 가격 수준 혹은 가격변화의 동질성 등을 고려하여 실증분석을 통해 기준을 도출하는 것이 정확할 수 있지만, 오랜 기간 시장에서 통용되고 있는 인식 또한 무시할 수 없다. 일반적으로 서울 오피스 시장의 하위 권역은 전통적인 업무 중심 지역으로 시청 등 주요 정부 기관과 기업들의 본사가 위치한 Central Business District(CBD), 벤처기업 및 IT산업을 중심으로 새로운 중심지로 성장해온 Gangnam Business District(GBD), 금융 관련 산업이 집중되어있는 Yeoido Business District(YBD)와 그 외 나머지 지역으로 나누어지는데 그 세부적인 구분 기준에 대해서는 실무적으로나 학술적으로나 명확하게 합의된 기준이 없다. <표 3>은 학술연구 및 민간업체의 오피스 시장 마켓리포트에서의 지역에 따른 서울시 오피스 하위시장 구분 기준을 정리한 것이다. 이들 사례를 살펴보면 학술연구를 위한 권역 구분은 거의 대부분이 자치구 단위로 묶어서 비교적 넓은 범위를 설정하고 있으며, 민간업체의 사례에서는 실제 재고 및 매매·임대 거래량이 많은 지역을 중심으로 보다 좁은 범위의 기준을 이용하고 있다. 본 연구는 이들 사례를 참고하고, 권역과 권역의 하위시장인 세부 지역을 나누고자 하는 점을 고려하여 <표 4> 및 <그림 1a>와 같이 4개의 권역 및 10개의 세부 지역으로 서울시 오피스 하위시장을 나누었다.
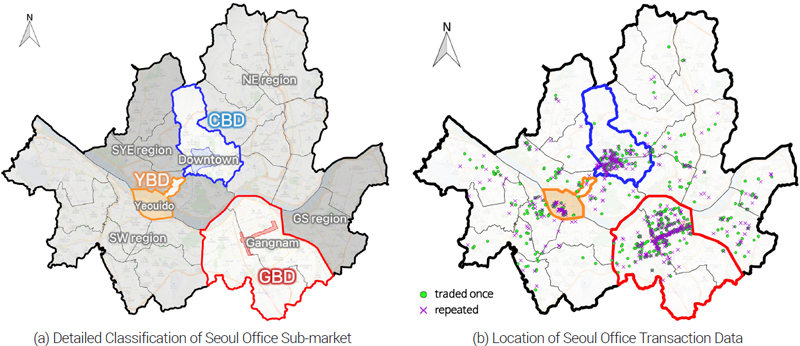
Seoul office sub-market classification and transaction data locationNote: The address information of the constructed transaction data was geocoded and mapped to QGIS
먼저 권역 구분은 권역별로 충분한 자료를 확보할 수 있는 수준에서 CBD(종로구, 중구), GBD(강남구, 서초구), YBD(영등포구 여의도동, 마포구 도화동, 공덕동, 신공덕동), Others(그 외 기타지역)으로 나누었다. 이들 4개 권역은 보다 세분화된 세부 지역으로 다시 구분하였는데, 민간업체의 오피스 마켓리포트4)를 참고하여 실무적으로 주요 업무권역으로 시장에서 인식되는 지역을 고려하여 10개의 세부 지역(도심5), 도심기타, 강남6), 강남기타, 여의도, 마포, GS지역, NE지역, SW지역, SYE지역)으로 나누었다.
3. 자료 구축
본 연구의 시간적 범위에 해당하는 2000년 1분기부터 2022년 2분기 사이에 서울시에서 계약된 오피스 빌딩의 실거래가 자료 1,735건을 수집하였다. 이상의 자료들 중 11건을 가격 이상치로 식별하여 제외한 1,724건의 거래자료 위치 분포는 <그림 1b>와 같다. 이 중 전체 지수 작성 기간 중 2회 이상 거래된 1,205건의 거래 사례를 반복매매 지수 산정을 위한 최종 자료로 구축하였다7). 지수 산정에 이용된 자료 이용률(총 자료 수 중 2회 이상 거래된 자료의 비율)은 69.9%로 나타났다. 이는 반복매매 모형을 이용할 때 1회 거래된 자료가 제외됨으로써 표본선택 편의가 나타날 수 있음을 지적한 Case et al.(1991), Gatzlaff and Haurin (1997), Hill et al.(2009)의 분석 자료에서 확인되는 자료이용률(각각 14.6%, 46.9%, 23.0%)에 비해 약 1.3~4.7배 더 높은 수치로 반복매매모형의 활용에 큰 문제가 없을 것으로 판단된다.
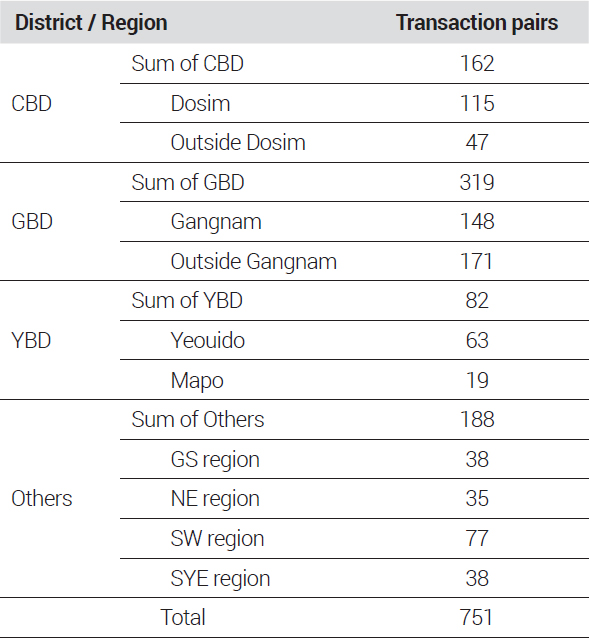
구축된 자료는 총 751개의 거래쌍8)을 구성하였으며 권역 및 세부 지역 구분에 따른 각각의 거래쌍 수는 <표 5>와 같이 나타났다. 권역별로는 GBD의 거래쌍이 가장 많았고, YBD는 82쌍으로 분기별 평균 1쌍에도 못 미치는 것으로 나타났다. 세부 지역별로 살펴보면, GBD는 기본적으로 타 권역에 비해 거래쌍 수가 많지만, YBD와 Others 권역은 세부 지역별로 나눌 경우 거래쌍 수가 40쌍에도 못 미치는 지역들이 존재하는 것으로 나타났다.
4. 분석 방법론
본 연구에서는 구조적 시계열 모형과 계층 모형을 활용하여 지수를 산정하고 비교하였다. 특히, 구조적 시계열 모형 중에서도 RW 모형을 활용하였다. 송영선 외(2021)의 연구 결과 세 가지 구조적 시계열 모형 중에서도 LLT 모형의 전반적인 지수 추정성능이 가장 우수한 것으로 나타났다. 그러나 LLT 모형은 가격 움직임의 전환점을 잘 포착하지 못하는 것으로 나타났으며, RW 모형이 시점별 가격 움직임의 변화를 더 잘 보여줄 수 있는 것으로 나타났다. 따라서 부동산 가격지수를 산정할 때 가격 움직임의 전환점을 잘 포착해내는 것이 중요하다는 점(Bokhari and Geltner, 2012)을 고려하여 본 연구에서는 세부적인 가격변동을 더 잘 관찰할 수 있는 RW 모형을 기초로 연구 모형을 구성하였다. RW 모형은 다음과 같이 나타낼 수 있다.
| (1) |
| (2) |
식 (1)은 가장 기본적인 형태의 반복매매 모형을 나타낸 것으로 t는 거래 시점을 나타내며, s, f는 각각 거래쌍 i의 두 번째(second), 첫 번째(first) 거래 시점을 의미한다. 따라서 pis(f)는 거래쌍 i의 두 번째(첫 번째) 시점의 로그 변환한 단위면적당 거래 가격을 나타낸다. 이에 따라 식 (1)의 좌변은 로그 변환한 거래쌍의 두 거래 시점 간 가격 변동률을 의미한다. rt(s,f)는 t(=s,f) 시점 시간효과를 의미하며, ϵit는 오차항을 나타낸다. 이때 오차항의 분포는 기본적으로 정규분포를 활용할 수 있으나 자료 수가 적은 경우에는 특정 이상치가 모형 내 다른 모수들의 추론에 영향을 미쳐 강건하지 못할 수 있다(Gelman et al., 2013, p.435). 이에 본 연구에서는 꼬리가 긴 t-분포를 이용하여 이상치의 영향을 줄이고 더 나은 추정이 가능하도록 하였다. 식 (2)는 시간효과 모수 rt의 랜덤워크 과정을 나타낸 것으로 t+1 시점 시간효과가 t 시점 시간효과를 평균으로, 를 분산으로 하는 정규분포로부터 결정되는 것을 의미한다. 이러한 인접 시점 간의 연결고리는 지수의 안정성을 개선할 수 있도록 하는 역할을 한다.
다음으로 RW 모형에 계층적 구조를 도입한 Francke and van de Minne(2017)의 계층 추세 반복매매 모형을 권역별 지수 산정에 이용하였다. 이를 위해 식 (1)의 시간효과 모수 rt를 g권역의 시간효과 에 대한 수식으로 표현하면 식 (3)과 같이 서울시의 평균적인 시간효과(μt′)와 하위 권역별 차이()의 합으로 이루어진 형태로 나타낼 수 있다. 이를 다시 식 (1)에 대입하면 식 (4)와 같이 계층 구조가 적용된 반복매매 모형 식이 도출된다.
| (3) |
| (4) |
| (5) |
| (6) |
결과적으로 거래쌍의 로그 가격변화율에 대한 모형에서 시간효과는 서울시 내 권역들이 공통적으로 가지는 평균적인 가격변동 추세(μ′s-μ′f)와 이로부터 분산된 하위 권역별 차이(-)로 구성된다. 이때 식 (2)와 동일하게 공통적인 추세와 권역별 차이를 나타내는 두 모수 모두 식 (5), (6)과 같이 랜덤워크 과정을 따르는 것으로 가정하였다.
한편, 세부 지역별 지수 산정에 바로 앞에서 소개한 계층 추세 반복매매 모형을 이용할 수 있다. 그러나 이 경우 각각의 세부 지역별로 자료 수가 부족하기 때문에 세부 지역별 차이에 대한 모수를 추정하는 데 이용되는 분산에 대한 정보가 안정적으로 이용되지 못하여 다소 신뢰도가 낮은 지수가 산정될 수 있다. 따라서 세부 지역별 지수 작성에는 2개의 계층 구조를 가지는 계층 모형을 활용하였다. 위에서 소개한 계층 모형이 세부 지역과 서울시 전체로 연결된 2수준 모형이라고 한다면, 세부 지역별 지수 산정에 이용할 모형은 세부 지역-권역-서울시로 이어지는 3수준 모형이다.
세부 지역별 지수 산정 시 2수준 모형을 이용한다면 식 (3)의 권역별 차이에 대한 모수는 α 세부 지역의 시간효과 (=μ′t+)로 다시 나타낼 수 있다. 여기에서 3수준 모형을 구성하기 위해 앞에서와 마찬가지로 세부 지역별 차이에 대한 모수는 다시 α 세부 지역이 속한 ga 권역별 공통적인 차이()와 이로부터 분산된 세부 지역별 차이()의 합으로 식 (7)과 같이 나타낼 수 있다. 이에 따라 3수준 계층 추세 반복매매 모형은 식 (8)과 같이 표현할 수 있다.
| (7) |
| (8) |
| (9) |
| (10) |
여기에서도 마찬가지로 식 (9), (10)과 같이 권역별 공통적인 차이()와 세부 지역별 차이()에 대한 모수는 랜덤워크 과정을 따르는 것으로 가정하였다.
이상의 연구 모형들은 실증분석에서 다음과 같이 활용하였다. 먼저, 권역별 지수 산정 시에는 식 (1), (2)의 RW 모형과 식 (4), (5), (6)의 hierarchical random walk(HRW) 모형을 이용하여 지수를 산정하고 비교하였다. 세부 지역별 지수 산정 시에는 HRW 모형9)과 식 (8), (5), (9), (10)의 multi-HRW10) 모형을 이용하였다.
다만, 기준시점(t=1) 대비 각 시점까지의 누적 변동률을 의미하는 시간효과 모수 rt, , 는 실제 지수 추정 시에는 관련된 추정 모수 rt, μ′t, , , 를 전 분기 대비 변동률을 의미하는 형태의 모수 βt(=rt-rt-1), μt(=μ′t-μ′t-1), (=-), (=-), (=-)로 바꾸어 추정하였다11). 이러한 모수 형태의 변형을 통해 보다 효율적인 추정과 표준오차의 감소 등을 기대할 수 있다.
본 연구에서는 과소거래 특성을 가진 자료의 한계를 극복하고자 베이지안 확률모형에 기초한 샘플링 기법인 Markov Chain Monte Carlo(MCMC)을 활용하여 지수를 추정하였다. 구체적으로는 Hamiltonian Monte Carlo(HMC) 알고리즘 중 현재 가장 발전된 형태인 No-U-Turn Sampler(NUTS)를 이용하였으며, 이를 위한 지원 도구로 R 4.2.1과 완전한 베이지안(full bayesian) 추론을 제공하는 프로그래밍 언어인 ‘rstan’ 및 ‘cmdstanr’ 패키지(Carpenter et al., 2017)를 이용하였다. MCMC 샘플링은 관련 선행연구(송영선 외, 2021; van de Minne et al., 2020)와 Stan Development Team(2022)의 권장 사항을 참고하여 4개의 chain을 이용하였으며, 각각의 chain별로 warmup 500회를 제외한 1,000회의 sampling을 진행하여 총 4,000개의 샘플링 결과로부터 모수를 추정하였다. MCMC 샘플링을 통해 모형 내 모든 모수들의 사후분포(posterior distribution)을 얻을 수 있는데 이 중 시간효과와 관련된 모수들의 사후평균을 이용하여 최종적으로 지수를 산정하였다.
MCMC 샘플링을 위해서는 모형 구성 후에 추가적으로 초모수(hyper-parameter)들의 사전분포(prior distribution)를 설정해야 한다. 가능도(likelihood)의 확률분포로 설정한 t-분포의 자유도는 선행연구(van de Minne et al., 2020)의 사례를 참고하여 지수분포(ν∼Exp(0.3))를 따르도록 가정하였으며, 나머지 초모수들은 앞서 나열한 수식에는 정규분포로 표현하였지만 실제 지수 추정 시에는 약정보적 사전분포12)로 많이 이용되는 확률분포의 형태 중 하나인 표준코시분포로 가정하였다.
Ⅳ. 지수 추정 결과
1. 권역별 지수 산정 결과
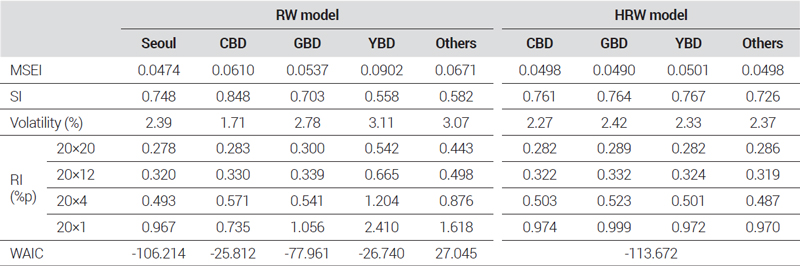
본 절에서는 서울시 오피스 권역별 가격지수를 산정하였다. 구체적으로는 권역별로 각각의 자료만을 이용하여 RW 모형으로 지수를 산정하고, 서울시 전체 자료를 모두 이용하여 HRW 모형으로 지수를 산정한 후 이 둘을 비교하였다.
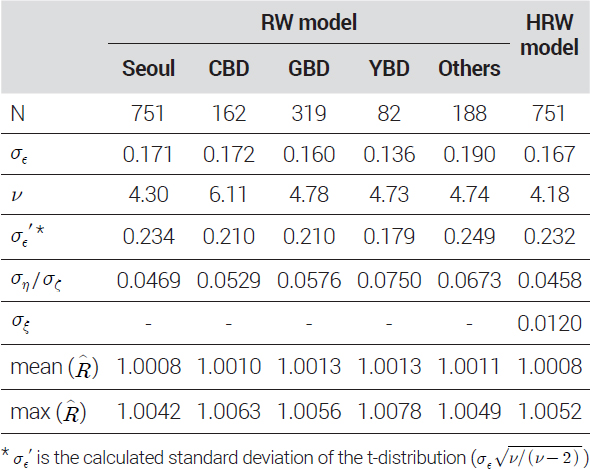
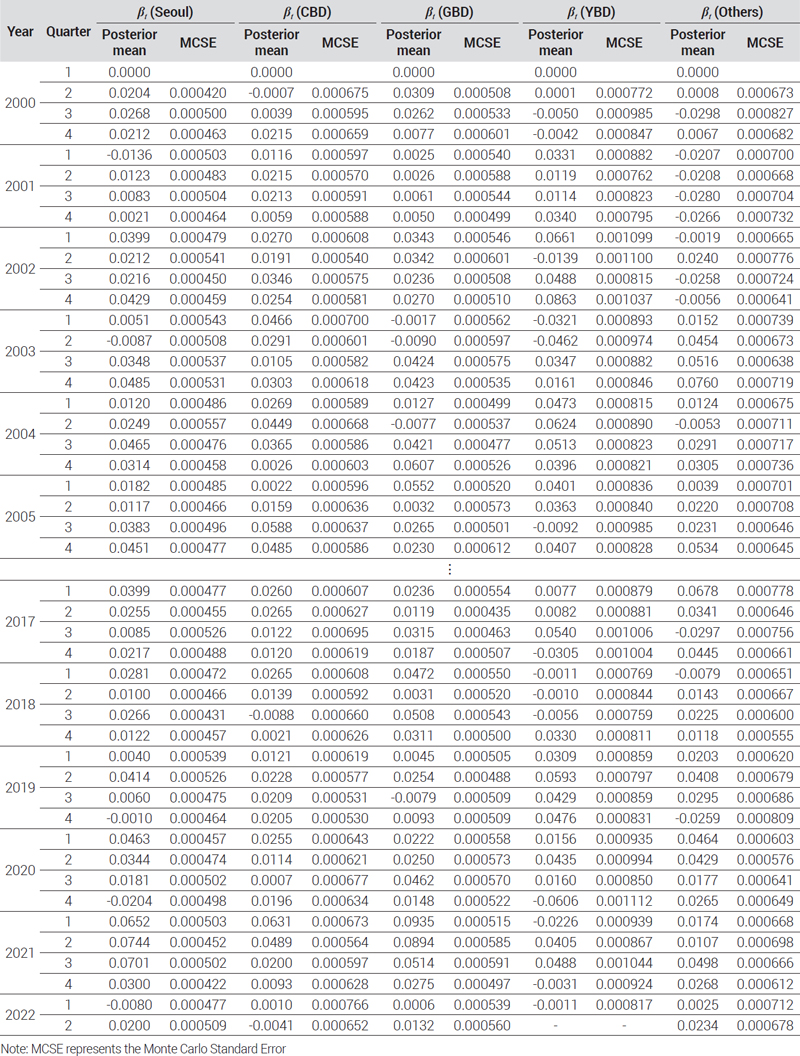
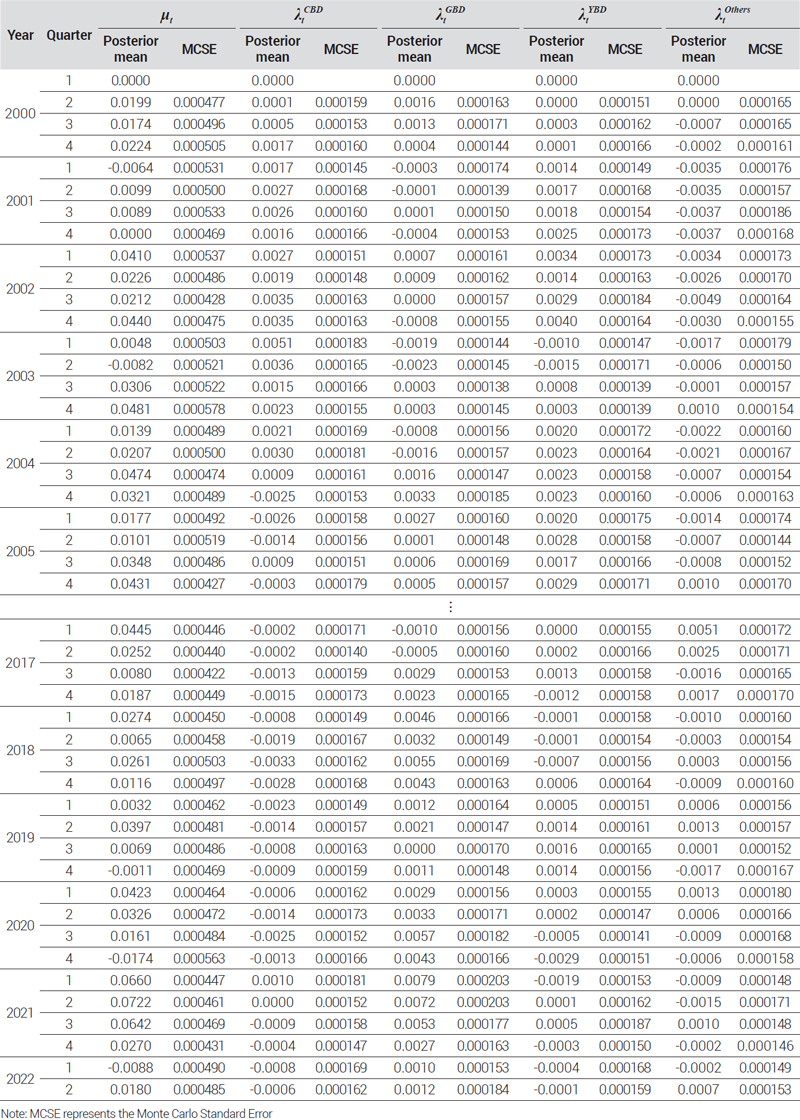
지수 모형의 시간 효과 모수에 대한 샘플링 결과13)는 초기 및 최근 5개년도 값을 <부록>에 별도로 수록하였으며, MCMC 샘플링 결과는 <표 6>에 요약하여 나타내었다. 먼저 MCMC 진단 결과에서 의 평균 및 최대값은 모두 1에 가까운 값으로 나타나 MCMC가 수렴하였음을 보여준다. 또한 N-eff는 모두 100%를 상회하는 값으로 나타나 효율적인 샘플링이 이루어졌음을 알 수 있다14). RW 모형에서 추정된 잡음, t-분포의 자유도와 분산 모수들의 사후평균(posterior mean)은 권역별로 서로 차이를 보이고 있다. CBD와 GBD는 유사하게 나타났으나, Others는 광범위하게 다양한 지역의 거래자료가 섞여 있는 탓에 잡음(σϵ′)이 상대적으로 크게 나타났다. 한편, HRW 모형에서 추정된 모수들의 사후평균은 RW 모형을 이용한 서울시 지수의 결과와 유사한 수준의 추정이 이루어졌음을 보여주고 있다. 0.012로 추정된 σξ는 RW 모형에는 포함되지 않는 모수로 HRW 모형에서 서울시 오피스 시장의 공통적인 가격변동 추세로부터 분산된 권역별 가격변동률을 만들어내는 역할을 할 것이다.
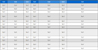
이상의 추정을 통해 작성한 권역별 가격지수를 그래프로 나타내면 <그림 2>와 같이 나타난다. 먼저 <그림 2a>의 RW 모형의 지수 그래프를 보면, 3개의 주요 권역은 서울시 전체와 비슷한 지수 추이를 보여주고 있으며, Others는 2003년까지의 하락으로 서울시 지수와는 동떨어진 수준의 값을 나타내고 있다. 지수의 움직임은 그래프만 보더라도 그리 안정적이지 못한 것으로 보여지는데, 이는 거래 자료가 없는 시점들이 존재하고, 모든 시점에 거래가 존재하더라도 그 수가 상당히 적기 때문이다. 특히, 특정 시점에 관측된 거래가 없는 경우에도 인접 시점 간 연결고리를 통해 지수의 추세를 바탕으로 보간하는 형태의 추정이 이루어지는 RW 모형의 구조적 특성으로 지수 추정이 가능함에도 불구하고, 거래 자료가 없거나 적은 시점의 추정치는 불안정할 수밖에 없을 것이다. 더욱이, 마지막 시점(2022년 2분기)의 거래가 존재하지 않는 YBD는 그 직전 시점까지만 지수가 추정된 한계가 있다. 이와 같이 거래자료가 적은 경우 지수 추정이 가능하다 할지라도 몇 안 되는 이상치에 영향을 크게 받을 수 있고, 주어진 소수의 데이터에만 적합한 결과를 얻어낼 가능성이 높다. 그러나 HRW 모형을 통해 얻은 <그림 2b>의 지수 그래프를 보면, 전반적으로 지수의 변동성이 낮아졌으며 서울시의 공통적인 가격변동 추세로부터 권역별로 분산된 지수를 추정할 수 있음을 보여주고 있다. 또한, RW 모형에서 추정되지 못한 YBD의 2022년 2분기 지수가 추정된 것을 확인할 수 있다. 이는 하위시장 간 평균적인 가격 움직임을 공유하고 수축 현상을 만들어내는 계층 모형의 특성에 의해 나타난 결과이며, Francke and van de Minne(2017)의 연구 결과와도 일치하는 지수가 산정되었음을 보여주고 있다. 결과적으로 부동산 시장에서의 공간적 특성에 따른 적절한 상·하위 계층 구조에 대한 가정이 전제된다면 보다 신뢰할 수 있는 지수를 얻을 수 있음을 보여주고 있다.
HRW 모형으로 얻어진 권역별 지수 추정성능의 개선은 <표 7>의 다양한 지표15)들을 통해서도 확인할 수 있다. 먼저 지수 추정 모수의 평균 표준오차를 통해 계산된 MSEI 값이 모든 권역에서 평균 24.3% 정도 감소하여 통계적 신뢰도가 높아졌음을 보여주고 있다. SI 값은 CBD를 제외한 3개 권역에서 지수 안정성이 높아졌음을 나타내고 있으며 이는 변동성16)의 감소로 이어진 것으로 나타났다. 지수 산정 모형을 선택함에 있어 중요한 지표인 지수 변화도 마찬가지로 CBD를 제외한 나머지 권역에서 크게 개선된 것을 확인할 수 있는데, CBD의 경우에도 최근 시점 지수변화는 HRW 모형이 조금 더 크게 나타나지만 장기적으로는 지수변화가 HRW 모형에서 더 작게 추정이 되는 것으로 나타났다. 모형의 예측력을 나타내는 WAIC 통계량은 직접적인 비교가 어렵지만, 4개 권역 각각에 대한 RW 모형의 WAIC 값에 차이가 크게 나타났고, 동일한 자료를 이용하였지만 서울시 전체 단일 지수를 추정한 결과와 비교하더라도 HRW 모형의 WAIC 값이 더 낮아 보다 나은 예측력을 가지고 있는 것으로 나타났다.
이상의 결과들을 종합해보면, 서울시 오피스 권역별 가격지수를 산정할 때 RW 모형에 비해 HRW 모형이 더 우수하다고 볼 수 있을 것이다. 먼저 이창무 외(2013), 송영선 외(2020) 등 지수 산정 연구에서 주요하게 활용하는 통계적 신뢰도 지표는 HRW 모형의 결과에서 큰 폭으로 높아진 것으로 나타났으며, 예측력 또한 HRW 모형이 더 높은 것으로 나타나 Francke and van de Minne(2017)의 연구 결과와 같이 자료 수가 적은 시장에서 계층 모형 활용의 이점인 과적합 개선을 통해 더 강건한 지수 산정이 가능할 수 있음을 간접적으로 보여주고 있다. 일정 부분 비슷한 의미를 가지고 있는 변동성과 지수 안정성 지표의 경우에는 Guo et al.(2014)에서 변동성이 낮을수록 실제 시장 가격의 움직임에 가까운 지수가 산정되었음을 보여준다고 설명하고 있지만 일정 수준 이상으로 변동성이 낮거나 지수 안정성이 높을 경우 시장의 전환점이 제대로 식별되지 않는 지수가 산정될 가능성이 있어 절대적인 지표로 삼기에는 한계가 있다. 그러나 <그림 2b>의 지수 그래프를 볼 때, 류강민·송기욱(2020)의 연구에서 대표적인 오피스 가격지수 전환점으로 관찰한 2008년 금융위기에 따른 가격 하락 전환점을 잘 포착하고 있는 것으로 나타나 과한 평활화에 따른 문제점은 우려할 수준이 아닌 것으로 보인다.
2. 세부 지역별 지수 산정 결과
다음으로 앞서 산정한 4개의 권역별 지수를 보다 세분화 된 지역별로도 나누어 HRW 모형과 multi-HRW 모형을 이용한 추정 결과를 비교하였다. 앞 절에서 이용한 HRW 모형을 이용하여 보다 세분화된 세부 지역별 가격지수의 산정이 가능할 것이다. 그러나 하위 지역을 세분화할 경우 지역별 거래 자료 수가 더욱 줄어들면서 해당 지역의 가격 움직임 특성이 충분히 반영되지 못할 가능성이 있다. 따라서 본 절에서는 추가적인 계층적 구조를 도입함으로써 지수의 추정성능을 보다 개선시킬 수 있는 방안을 제시하고 비교를 통해 확인하고자 한다.
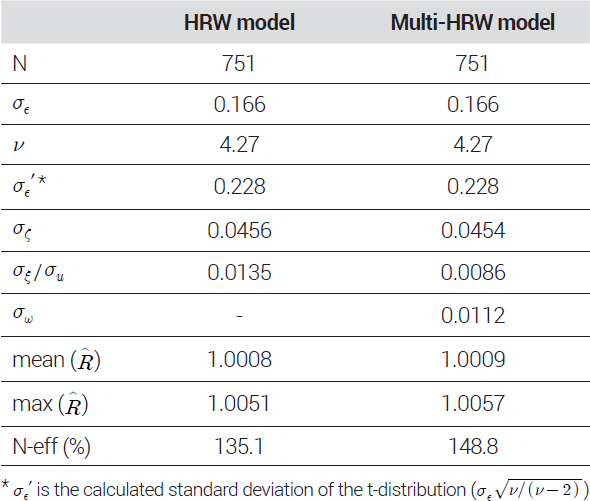
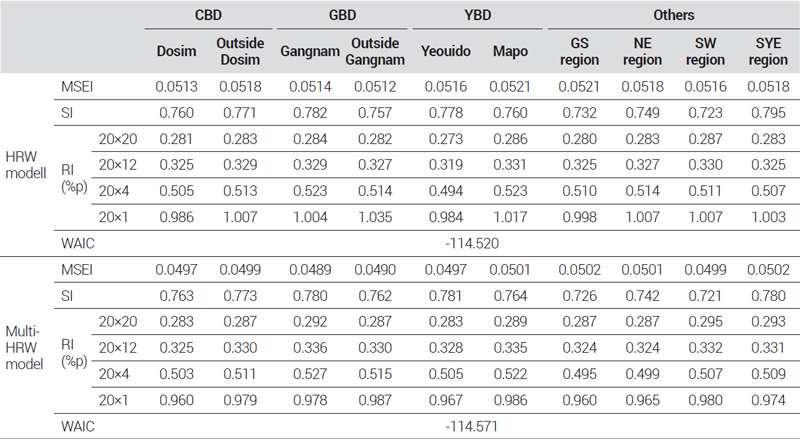
<표 8>의 MCMC 진단 결과에서 두 모형의 MCMC 샘플링 진단 결과 모두 효율적인 추정이 이루어졌음을 확인할 수 있었다. 두 모형에서 공통적으로 포함하고 있는 모수들의 사후평균은 거의 유사한 수준으로 나타나 시장 전체에 대한 추정은 동일하게 이루어졌으나, HRW 모형의 σξ는 0.0135, multi-HRW 모형의 σu, σw는 0.0086, 0.0112로 각각 추정되었다. 이와 같이 권역별 차이를 나타내는 분산모수 σξ, σu가 두 모형에서 서로 다른 사후평균 값을 보이는 것은 식 (7)에서 나타낸 것과 같이 식 (8)의 δ′t가 α′t와 함께 식 (4)의 λ′t를 구성하는 권역별 공통 추세를 나타내는 모수로 각각의 모형에서 가지는 의미가 다르기 때문이다.
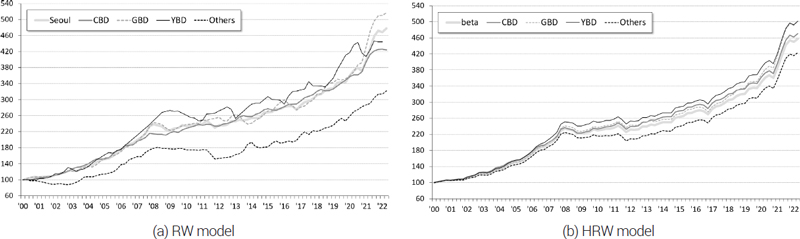
<그림 3>은 하위 세부 지역의 지수 작성 결과를 모형별 비교가 가능하도록 권역별로 묶어서 나타낸 것이다. 그래프를 보면 CBD의 경우 두 모형 모두 거의 비슷한 그래프 추이를 나타내고 있으나 GBD, YBD에서는 강남기타 지역과 마포 지역의 지수가 모형별로 소폭의 차이를 보이고 있다. Others에서는 주요 권역들에 비해 비교적 큰 차이가 나타나는데, HRW 모형으로 산정한 지수가 누적적인 가격 상승 폭이 크고, 세부 지역별 차이도 더 크게 나타난 것으로 확인된다. 기본적으로 거래 빈도가 적은 과소거래시장이기 때문에 참값이 무엇인지 정확하게 알 수는 없으나, HRW 모형의 경우 10개의 세부 지역별로 나누어 권역에 비해 자료 수가 훨씬 적기 때문에 상대적으로 불안정한 결과로 이어져 나타난 차이로 판단된다. 실제로 <표 8>의 세부 지역별 분산 모수의 값을 <표 6>의 권역별 지수 추정 결과와 비교할 때, 권역별 분산 모수에 비해 세부 지역별 분산 모수가 조금 더 크게 추정된 것을 확인할 수 있다.
지수의 추정성능과 관련된 지표는 <표 9>와 같이 나타났다. 세부 지역들의 평균적인 지표 수준에서 비교해보면, 지수의 안정성은 HRW 모형에서 조금 더 높은 것으로 나타났으나 유의미한 수준의 차이는 아니다. 반면에 통계적 신뢰도, 지수 변화, 모형의 예측력은 multi-HRW 모형이 보다 나은 지수 추정성능을 가지고 있는 것으로 나타났다. 그중 강남과 강남기타 지역은 MSEI 값이 각각 4.9%, 4.5% 감소하여 타 지역에 비해 통계적 신뢰도 향상이 크게 나타났는데, 특히 강남 지역은 두 모형에서 지수가 거의 유사한 값으로 산정되었음에도 불구하고 이와 같은 차이가 나타났다. 지수 변화 지표의 경우에는 장기적인 지수 변화는 HRW 모형이 조금 더 적은 것으로 나타났지만, 유의미한 수준의 차이는 아닌 것으로 판단되며 오히려 단기적인 지수 변화는 multi-HRW 모형이 더 적은 것으로 나타났다. 이는 앞서 두 모형 간 지수의 차이를 설명한 것과 같이 HRW 모형의 경우 자료 수가 적은 세부 지역 단위에서 바로 분산에 관한 정보를 취하여 추정이 이루어지기 때문에 최근 시점에 거래 정보가 없거나 부족하여 불안정한 결과로 이어질 수 있는 반면에 multi-HRW 모형에서는 권역 단위로 집계된 분산 정보를 활용하기 때문에 상대적으로 최근 시점에 대하여 정확한 분산 추정이 가능한 특성에 의한 결과로 판단된다. 결론적으로 HRW 모형을 통해 지수 추정 결과의 개선이 어느 정도 가능함에도 불구하고 자료 수 부족에 따른 불안정성을 2개의 계층적 구조를 적용하여 추가적으로 개선할 수 있음을 보이고 있다.
Ⅴ. 결 론
본 연구에서는 거래 빈도가 적은 오피스 시장을 대상으로 하여 기존의 국내 연구들(최성호 외, 2010; 류강민 외, 2017; 황규완·손재영, 2017)에서 한계점으로 지적되었던 세분화된 지수를 산정하는 방안을 제시하였다. 이를 위해 베이지안 계층 모형을 활용하였는데 기존에 제안되었던 다양한 방법론들과 비교하여 관측된 거래 사례에만 잘 적합한 것이 아닌 실제 시장 상황을 보다 잘 보여줄 수 있으며, 거래가 관측되지 않은 시점에 대해서도 지수 추정이 가능하다는 장점이 있다. 연구에서 제시한 하위 지수 모형의 활용 이점을 확인하기 위해서는 지수의 형태와 전통적인 추정성능에 대한 지표뿐만 아니라 지수의 활용성 측면에서 중요한 지수 변화 등을 함께 비교하여 계층 모형의 이점들을 실증적으로 확인하였다. 또한, 다수의 기존 연구들에서 활용된 지역적 구분에 해당하는 4개의 권역별로만 나누는 것이 아닌 보다 세분화된 지역별 지수를 산정하는 방안을 모색하였는데, 기본적인 형태의 모형과 비교하여 본문에서 제안한 모형이 통계적으로도 더 나은 추정이 가능하다는 결과를 나타내었다.
그러나 본 연구는 다음과 같은 몇 가지 한계점을 가진다. 첫 번째로 각종 지표들의 비교를 통해 여러 측면에서 연구 모형이 하위시장 지수의 추정성능을 개선할 수 있음을 보였으나, 본 연구에서 지수 작성 결과가 실제로 시장의 가격 움직임을 적절하게 보여주고 있는지에 대한 검증이 부족하다. 두 번째는 본 연구의 지수 모형에 기초가 되는 반복매매모형의 특성으로 인해 나타나는 한계이다. 앞서 투자자의 실제 투자 경험(매수 및 매도)을 직접적으로 반영할 수 있는 이점이 있다고 소개하였으나, 다수의 연구들을 통해 1회 거래된 사례, 거래가 이루어지지 않은 표본의 누락에 따른 표본 선택 편의의 발생 가능성이 꾸준히 제기되어져 왔다(Clapp and Giaccotto, 1992; 이영유·이상경, 2013). 또한 반복매매모형의 구조적 특성으로 지수 변화가 불가피하게 발생하게 되는데, 이는 시장 투자자들에게 혼란을 야기하거나 파생상품에의 활용에 제약 요인으로 작용할 수 있는 문제가 있다. 물론 지수 변화는 보다 신뢰성 높은 지수를 추정해나가는 과정에서 필수적으로 나타나는 특성이기 때문에 수용하고 있지만 그 폭을 최소화하는 노력은 필요하다. 세 번째, 연구 모형에 하위시장 간 특성의 차이를 반영하는 등의 세부 사항에 대한 논의가 부족하다. 본 연구에서 제시한 모형은 권역별로 세부 지역들의 가격 움직임에 대한 분산이 동일한 것으로 가정하였으나, 실제로는 권역별로 가격 움직임에 차이가 존재하거나 권역 및 세부 지역의 구분이 적절하게 이루어지지 않았다면 이는 시장에 잘 맞지 않는 모형일 가능성이 있다.
그럼에도 본 연구는 다음과 같은 점에서 의의를 가지고 있다. 먼저 연구의 한계점으로 시장의 가격 움직임을 제대로 표현하고 있는가에 관해 지적하였으나 본 연구에서 활용한 계층 모형은 전통적인 지수 산정 모형과 달리 관측치를 가장 정확하게 표현하는 것이 아니라 시장에서 완전히 포착되지 못한 가격 움직임을 예측하여 보여주는 성격이 보다 강하다. 특히 오피스 시장의 경우 타 부동산 유형에 비해 이질적인 특성을 가지고 있고 거래 빈도가 낮아 이를 직접적으로 검증하는 것은 불가능하다. 오히려 본 연구에서는 계층 모형의 활용으로 기존 방법론으로 산정되는 지수의 수용 불가능한 변동성의 수준을 낮추면서도 통계적으로 신뢰도가 높은 지수 산정이 가능하다는 점을 몇 가지 지표들을 통해 수치적으로 보여주고 있다.
다음으로 본 연구에서 제안한 지수 세분화 방안은 무엇보다도 연구자의 연구 결과 및 연역적 선택에 따라 자유롭게 모형 수정이 가능한 이점을 가지고 있는 stan을 이용한 MCMC 샘플링 기법을 활용하였기에 가능했다. 이러한 방법론을 통해 향후 관련 연구에서도 주거용 및 상업용부동산의 다양한 유형과 각기 다른 하위시장의 구분에 활용하여 발전시킬 수 있는 가능성을 열어 두고, 기본 방향을 제시하였다는 점에서 학술적 의의가 있다.
이외에 오피스 시장의 투자 규모가 지속적으로 커지고 있고, 부동산 간접투자 시장이 점차 확대되면서 기관투자자뿐만 아니라 개인투자자 또한 큰 관심을 가지고 있으나 주거용 부동산과 달리 상업용부동산 시장은 여전히 정보 접근이 용이하지 않은 상황이다. 이러한 상황에서 세분화된 하위시장 지수는 투자자의 투자 의사 결정에 도움을 주고 투자 성과를 평가할 수 있는 다양한 시장 정보를 제공한다는 점에서 실무적으로도 의의가 있다. 구체적으로는 과거의 추이를 기반으로 한 직접적인 성과 평가와 단기적인 예측을 통한 의사결정이 가능하고, 더 나아가서는 부동산의 가치 평가에 기초 지수로 활용되어 투자수익률의 측정까지도 가능하다.
따라서 향후에는 연구 모형과 상·하위시장 간 관계에 대한 보다 구체적인 고민과 더 나아가서 정확한 하위시장 구분 기준에 대한 연구가 이루어진다면 보다 신뢰할 수 있는 지수 산정이 가능할 것이다.
Acknowledgments
본 논문은 2021년 한국부동산분석학회 상반기 학술대회에서 발표한 내용의 일부를 수정·보완하여 작성하였음.
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
References
-
교보리얼코, 2022. 「2022년 3분기 오피스 마켓리포트」, 서울.
Kyoborealco, 2022. 2022. 3Q Office Market Report, Seoul. -
권민성·최우현·송영선·이창무, 2022. “계층적 베이지안 추론을 통한 아파트 단지별 실거래 기반 시세 개발”, 「부동산학연구」, 28(4): 39-54.
Kwon, M.S., Choi, W.H., Song, Y.S., and Lee, C.M., 2022. “Study of Apartment Complex Market Price Based on Hierarchical Bayesian Inference”, Journal of the Korea Real Estate Analysts Association, 28(4): 39-54. [ https://doi.org/10.19172/KREAA.28.4.3 ]
-
류강민·박수훈·이창무, 2011. “부동산 파생상품 개발을 위한 오피스 가격지수 산정”, 「선물연구」, 19(4): 363-387.
Ryu, K.M., Park, S.H., and Lee, C.M., 2011. “Office Price Index for Derivative Using S&P/Case-Shiller Estimator”, Journal of Derivatives and Quantitative Studies, 19(4): 363-387. [ https://doi.org/10.1108/JDQS-04-2011-B0002 ]
-
류강민·송기욱, 2020. “반복매매모형을 활용한 서울시 오피스 벤치마크 가격지수 개발 및 시험적 적용 연구”, 「LHI Journal」, 11(2): 33-46.
Ryu, K.M. and Song, K.W., 2020. “The Development and Application of Office Price Index for Benchmark in Seoul using Repeat Sales Model”, LHI Journal of Land, Housing, and Urban Affairs, 11(2): 33-46. -
류강민·한제선·정상준·이창무, 2017. “TPL을 이용한 일단위 실거래 가격지수 산정방법에 관한 연구”, 「주택연구」, 25(2): 5-23.
Ryu, K.M., Han, J.S., Jung, S.J., and Lee, C.M., 2017. “Daily Home Price Index Methodology using TPL (Triple Power Law)”, Housing Studies Review, 25(2): 5-23. [ https://doi.org/10.24957/hsr.2017.25.2.05 ]
-
박치형, 2012. “주택투자에서 지역과 평형을 고려한 포트폴리오의 위험분산효과”, 「지리학논총」, 58: 29-48.
Park, C.H., 2012. “Risk Diversification Effects Based on Region and Housing Size in Housing Investment”, Journal of Geography, 58: 29-48. -
박헌수, 2007. “거래빈도가 낮은 시장에서의 실거래 부동산 가격지수 작성에 관한 연구: 강남구를 대상으로”, 「부동산학연구」, 13(3): 187-200.
Park, H.S., 2007. “A Study on the Construction of a Transaction-Based Real Estate Price Index for Thin Markets in Gangnam-Gu, Seoul”, Journal of the Korea Real Estate Analysts Association, 13(3): 187-200. -
송영선·신혜영·이창무, 2021. “부동산 과소거래시장에 대한 안정적인 실거래가 지수 산정에 관한 연구”, 「부동산학연구」, 27(4): 21-40.
Song, Y.S., Shin, H.Y., and Lee, C.M., 2021, “A Stable Transaction Based Price Index for Real Estate Thin Market”, Journal of the Korea Real Estate Analysts Association, 27(4): 21-40. [ https://doi.org/10.19172/KREAA.27.4.2 ]
-
송영선·윤명탁·이창무, 2020. “아파트 하위시장 실거래가 지수 산정방식 비교 연구”, 「부동산분석」, 6(3): 1-19.
Song, Y.S., Yun, M.T., and Lee, C.M., 2020. “A Study on the Comparison of the Home Price Index Methodology based on Transaction Price in the Apartment Sub-Market”, Journal of Real Estate Analysis, 6(3): 1-19. [ https://doi.org/10.30902/jrea.2020.6.3.1 ]
-
이영유·이상경, 2013. “표본선택편의를 고려한 오피스 매매가격 결정요인 분석 및 매매가격지수 산정”, 「부동산학연구」, 19(1): 83-96.
Lee, Y.Y. and Lee, S.K., 2013. “Price Determinants and Transaction-Based Price Indices under Sample Selection Bias in the Seoul Metropolitan Office Market”, Journal of the Korea Real Estate Analysts Association, 19(1): 83-96. -
이준용·이현석, 2008. “외국자본의 서울 오피스빌딩 투자에 대한 입지적 선호요인 연구”, 「국토계획」, 43(7): 135-148.
Lee, J.Y. and Lee, H.S., 2008. “A Study on Locational Preference Factors of Foreign Capital for Seoul Office Building Investment”, Journal of Korea Planning Association, 43(7): 135-148. -
이창무·김용경·배익민, 2007. “반복매매모형을 이용한 아파트 실거래지수 운영특성 분석”, 「부동산학연구」, 13(2): 21-40.
Lee, C.M., Kim, Y.K., and Bae, I.M., 2007. “Operational Characteristics of Repeat Sales Price Indices Using Transaction Sales and Chonsei Prices of Apartments”, Journal of the Korea Real Estate Analysts Association, 13(2): 21-40. -
이창무·류강민·김지연, 2013. “Quantile Regression을 이용한 반복매매지수 산정에 관한 연구”, 「부동산학연구」, 19(4): 27-40.
Lee, C.M., Ryu, K.M., and Kim, J.Y., 2013. “A Repeat Sales Price Index Using Quantile Regression”, Journal of the Korea Real Estate Analysts Association, 19(4): 27-40. -
이창무·이재우, 2005. “서울시 오피스 임대시장구조 실증분석”, 「국토계획」, 40(2): 207-221.
Lee, C.M. and Lee, J.W., 2005. “An Analysis of Structure of the Office Rental Market in Seoul”, Journal of Korea Planning Association, 40(2): 207-221. -
이현석·이준용, 2010. “권역별 오피스 임대료의 순환과 조정과정 분석”, 「부동산학연구」, 16(3): 83-98.
Lee, H.S. and Lee, J.Y., 2010. “An Analysis on the Cycle and the Adjustment Process of Office Rent by Regions”, Journal of the Korea Real Estate Analysts Association, 16(3): 83-98. -
장래석·엄현포·최창규, 2021. “권역별 특성에 따른 대규모 오피스 빌딩의 순 실효 임대료에 영향을 미치는 주변 요인 분석: 서울시 권역별 오피스 빌딩의 차이를 중심으로”, 「국토계획」, 56(5): 199-214.
Jang, R.S., Eom, H.P., and Choi, C.G., 2021. “Analysis of Factors Affecting the Net Effective Rent of Prime Office Buildings by Region in Seoul: Focus on the Difference between CBD, GBD, YBD Office Markets in Seoul”, Journal of Korea Planning Association, 56(5): 199-214. [ https://doi.org/10.17208/jkpa.2021.10.56.5.199 ]
-
정유신, 2010. “서울시 오피스빌딩의 임대료 결정요인, 지수 및 투자수익률에 관한 연구”, 경기대학교 박사학위논문.
Jung, Y.S., 2010. “An Empirical Study on the Determinants on Rents, Index and Investment Yields of Commercial Property in Seoul”, Ph.D. Dissertation, Kyonggi University -
정호진, 2011. “오피스 빌딩의 자본수익률 영향요인에 관한 연구: 서울시 오피스 빌딩을 사례로”, 전주대학교 박사학위논문.
Jeong, H.J., 2011. “An Analysis on the Factors Affecting the Capital Value Return: The Case Study of the Office Buildings in Seoul”, Ph.D. Dissertation, Jeonju University. -
젠스타메이트, 2022. 「Office Market Report (2022 Q3)」, 서울.
GenstarMate, 2022. Office Market Report(2022 Q3), Seoul. -
차승호, 2020. “베이지안 추세 반복매매모형을 활용한 실거래가 기반 토지가격지수 개발에 관한 연구”, 한양대학교 석사학위논문.
Cha, S.H., 2020. “Land Sales Price Index Using Bayesian Repeat Sales Models Incorporating a Trend Component”, Master’s Degree Dissertation, Hanyang University. -
최막중, 1995. “서울시 오피스 시장의 특성과 추이 및 전망”, 「국토계획」, 30(6): 143-159.
Choi, M.J., 1995. “The Seoul Office Market: Characteristics, Trend, and Prospect”, Journal of Korea Planning Association, 30(6): 143-159. -
최성호·류강민·이건우·이창무, 2010. “반복매매모형을 활용한 오피스 매매가격지수에 관한 연구”, 「국토계획」, 45(7): 119-131.
Choi, S.H., Ryu, K.M., Lee, G.W., and Lee, C.M., 2010. “A Repeat Sales Price Indices for Office Market Using Transaction Data”, Journal of Korea Planning Association, 45(7): 119-131. -
한화호텔&리조트 에스테이트 부문, 2022. 「Office Market Report 2022.3Q」, 서울.
Hanwha Hotels & Resorts Estate Division, 2022. Office Market Report 2022.3Q, Seoul. -
허진호, 1998. “서울시 오피스 임대시장 지역간 차이에 관한 연구”, 한양대학교 석사학위논문.
Heo, J.H., 2020. “Regional Differences in Rent and Other Characteristics of the Seoul Office Rental Market: Focus on Rent of Office Market”, Master’s Degree Dissertationn, Hanyang University. -
홍자영·이용만, 2003. “부동산투자의 지역별 포트폴리오 효과”, 「부동산연구」, 13(1): 181-195.
Hong, J.Y. and Lee, Y.M., 2003. “Geographical Diversification in Real Estate Portfolio”, Korea Real Estate Review, 13(1): 181-195. -
황규완·손재영, 2017. “MIT/CRE 2단계 추정법을 활용한 서울 오피스 가격지수 산출에 관한 연구”, 「주택연구」, 25(1): 151-175.
Hwang, G.W. and Son, J.Y., 2017. “Development of a Office Price Index in Seoul Using Two Stage Estimation Methodology Developed by MIT/CRE”, Housing Studies Review, 25(1): 151-175. [ https://doi.org/10.24957/hsr.2017.25.1.151 ]
-
KB국민은행, 2022. 「KB 오피스 투자지수_2022년 3분기」, 서울.
KB Kookmin Bank, 2022. KB Office Investment Index, 2022. 3Q, Seoul. -
Kruschke, J.K., 2018. 「R, JAGS, Stan을 이용한 베이지안 데이터 분석 바이블 (제2판)」, 최정렬 역, 파주: 제이펍.
Kruschke, J.K., 2018. Doing Bayesian Data Analysis: A Tutorial with R, JAGS, and Stan(2nd ed.), Translated by Choi, J.R., Paju: Jpub. -
Bailey, M.J., Muth, R.F., and Nourse, H.O., 1963. “A Regression Method for Real Estimate Price Index Construction”, Journal of the American Statistical Association, 58: 933-942.
[https://doi.org/10.1080/01621459.1963.10480679]

-
Bokhari, S. and Geltner, D., 2012. “Estimating Real Estate Price Movements for High Frequency Tradable Indexes in a Scarce Data Environment”, The Journal of Real Estate Finance and Economics, 45(2): 522-543.
[https://doi.org/10.1007/s11146-010-9261-4]

-
Bourassa, S.C. and Hoesli, M., 2017. “High-frequency House Price Indexes with Scarce Data”, Journal of Real Estate Literature, 25(1): 207-220.
[https://doi.org/10.1080/10835547.2017.12090448]

-
Carpenter, B., Gelman, A., Hoffman, M.D., Lee, D., Goodrich, B., Betancourt, M., Brubaker, M.A., Guo, J., Li, P., and Riddell, A., 2017. “Stan: A Probabilistic Programming Language”, Journal of Statistical Software, 76(1): 1-32.
[https://doi.org/10.18637/jss.v076.i01]

-
Case, B., Pollakowski, H.O., and Wachter, S.M., 1991. “On Choosing among House Price Index Methodologies”, AREUEA Journal, 19(3): 286-307.
[https://doi.org/10.1111/1540-6229.00554]

-
Chegut, A.M., Eichholtz, P.M.A., and Rodrigues, P., 2013. “The London Commercial Property Price Index”, Journal of Real Estate Finance and Economics, 47: 588-616.
[https://doi.org/10.1007/s11146-013-9429-9]

-
Clapp, J.M. and Giaccotto, C., 1992. “Estimating Price Indices for Residential Property: A Comparison of Repeat Sales and Assessed Value Methods”, Journal of Real Estate Finance and Economics, 5(4): 357-374.
[https://doi.org/10.1007/BF00174805]

-
Deng, Y. and Quigley, J.M., 2008. “Index Revision, House Price Risk, and the Market for House Price Derivatives”, The Journal of Real Estate Finance and Economics, 37(3): 191-209.
[https://doi.org/10.1007/s11146-008-9113-7]

-
Francke, M.K., 2010. “Repeat Sales Index for Thin Markets: A Structural Time Series Approach”, The Journal of Real Estate Finance and Economics, 41(1): 24-52.
[https://doi.org/10.1007/s11146-009-9203-1]

-
Francke, M.K. and van de Minne, A., 2017. “The Hierarchical Repeat Sales Model for Granular Commercial Real Estate and Residential Price Indices”, The Journal of Real Estate Finance and Economics, 55(4): 511-532.
[https://doi.org/10.1007/s11146-017-9632-1]

-
Francke, M.K. and Vos, G.A., 2004. “The Hierarchical Trend Model for Property Valuation and Local Price Indices”, The Journal of Real Estate Finance and Economics, 28(2/3): 179-208.
[https://doi.org/10.1023/B:REAL.0000011153.04496.42]

-
Gatzlaff, D.H. and Haurin, D.R., 1997. “Sample Selection Bias and Repeat-sales Index Estimates”, The Journal of Real Estate Finance and Economics, 14: 33-50.
[https://doi.org/10.1023/A:1007763816289]

-
Gelman, A. and Rubin, D.B., 1992. “Inference from Iterative Simulation Using Multiple Sequences”, Statistical Science, 7(4): 457-472.
[https://doi.org/10.1214/ss/1177011136]

-
Gelman, A., Carlin, J.B., Stern, H.S., Dunson, D.B., Vehtari, A., and Rubin, D.B., 2013. Bayesian Data Analysis (3rd ed.), Boca Raton, FL: CRC Press.
[https://doi.org/10.1201/b16018]

- Geltner, D.M., Miller, N.G., Clayton, J., and Eichholtz, P., 2014. Commercial Real Estate, Analysis & Investments, (3rd ed.), Wisconsin, WI: Mbition LLC.
-
Goetzmann, W.N., 1992. “The Accuracy of Real Estate Indices: Repeat Sale Estimators”, Journal of Real Estate Finance and Economics, 5(1): 5-53.
[https://doi.org/10.1007/BF00153997]

-
Guo, X., Zheng, S., Geltner, D., and Liu, H., 2014. “A New Approach for Constructing Home Price Indices: The Pseudo Repeat Sales Model and Its Application in China”, Journal of Real Housing Economics, 25: 20-38.
[https://doi.org/10.1016/j.jhe.2014.01.005]

-
Hill, R.J., Melser, D., and Syed, I., 2009. “Measuring a Boom and Bust: The Sydney Housing Market 2001-2006”, Journal of Housing Economics, 18(3): 193-205.
[https://doi.org/10.1016/j.jhe.2009.07.010]

-
Hill, R.J., Scholz, M., Shimizu, C., and Steurer, M., 2022 “Rolling-Time-Dummy House Price Indexes: Window Length, Linking and Options for Dealing with Low Transaction Volume”, Journal of Official Statistics, 38(1): 127-151.
[https://doi.org/10.2478/jos-2022-0007]

-
Lancaster, K.J., 1966. “A New Approach to Consumer Theory”, Journal of Political Economy, 74(2): 132-157.
[https://doi.org/10.1086/259131]

-
McElreath, R., 2020. Statistical Rethinking: A Bayesian Course with Examples in R and Stan (2nd ed.), Boca Raton, FL: CRC Press.
[https://doi.org/10.1201/9780429029608]

-
McMillen, D.P. and Dombrow, J., 2001. “A Flexible Fourier Approach to Repeat Sales Price Indexes”, Real Estate Economics, 29(2): 207-225.
[https://doi.org/10.1111/1080-8620.00008]

-
McMillen, D.P. and McDonald, J., 2004. “Reaction of House Prices to a New Rapid Transit Line: Chicago’s Midway Line, 1983-1999”, Real Estate Economics, 32(3): 463-486.
[https://doi.org/10.1111/j.1080-8620.2004.00099.x]

-
Rosen, S., 1974. “Hedonic Prices and Implicit Markets: Product Differentiation in Pure Competition”, Journal of Political Economy, 82(1): 34-55.
[https://doi.org/10.1086/260169]

-
Schwann, G.M., 1998. “A Real Estate Price Index for Thin Markets”, The Journal of Real Estate Finance and Economics, 16(3): 269-287.
[https://doi.org/10.1023/A:1007719513787]

-
Shimizu, C., Takatsuji, H., Ono, H., and Nishimura, K.G., 2010. “Structural and Temporal Changes in the Housing Market and Hedonic Housing Price Indices”, International Journal of Housing Markets and Analysis, 3(4): 351-368.
[https://doi.org/10.1108/17538271011080655]

-
van de Minne, A., Francke, M., Geltner, D., and White, R., 2020. “Using Revisions as a Measure of Price Index Quality in Repeat-Sales Models”, The Journal of Real Estate Finance and Economics, 60(4): 514-553.
[https://doi.org/10.1007/s11146-018-9692-x]

-
Vehtari, A., Gelman, A., and Gabry, J., 2017. “Practical Bayesian Model Evaluation using Leave-one-out Cross-validation and WAIC”, Statistics and Computing, 27(5): 1413-1432.
[https://doi.org/10.1007/s11222-016-9696-4]

- Watanabe, S., 2010. “Asymptotic Equivalence of Bayes Cross Validation and Widely Applicable Information Criterion in Singular Learning Theory”, Journal of Machine Learning Research, 11: 3571-3594.
-
통계청, “국가통계포털”, 2023.2.23. 읽음. https://kosis.kr/index/index.do
Statistics Korea, “Korean Statistical Information Service”, Accessed February 23, 2023. https://kosis.kr/index/index.do -
한국부동산원, “부동산통계정보시스템(R-ONE)”, 2022.3.7. 읽음. https://www.reb.or.kr/r-one/main.do
Korea Real Estate Board, “Real Estate Statistical Information System (R-ONE)”, Accessed March 7, 2022. https://www.reb.or.kr/r-one/main.do - Stan Development Team, 2022. Stan User’s Guide Version 2.31, Accessed December 19, 2022. https://mc-stan.org/