
Print publication date Feb 2014
Congestion Tolls, Transport Capacity, and Financing: A General Equilibrium Approach
One treatment of congestion tolls is that when designed appropriately toll revenues just cover the capacity cost of transport facilities. We reexamine this proposition while embedding the transport network in the land market. We considerably extend the setting of the standard network model in several important ways and confirm the validity of the self-financing rule. At the same time, we extend the applicability of Yu and Rhee's (2011) analytical methodology for the Anas type land-use and transportation models.
Keywords:
Congestion Tolls, Transport Capacity, Financing, Land Use- Transportation Model, General Equilibrium, 혼잡통행료, 교통시설의 규모, 재원조달, 토지이용-교통모형, 일반균형Ⅰ. 서 론
교통시설의 설치와 운영에 소요되는 재정을 일반재원을 통해 조달하는 경우, 재원조달을 위해 동원되는 과세로 인해 상대가격이 변하게 되고 그 결과 자원배분이 왜곡되는 부작용이 발생한다. 이뿐만 아니라 교통시설을 이용하지 않는 사람들에게도 조세가 부과되어 형평성 측면에서도 문제가 발생하게 된다. 이때 수익자 부담의 원칙의 따라 확보된 재원을 교통체계의 건설과 운영에 소요되는 재원으로 활용하는 방안은 효율성과 형평성 양측면에서 일반재원에 의한 재원조달 방식보다 우월하다고 말할 수 있다.
본 논문은 교통시설 소요재정을 혼잡통행료를 통해 조달할 때, 과연 이러한 조달방식이 효율적인지 그리고 교통시설의 소요재정을 과부족 없이 충당할 수 있는지에 대해 분석한다. 이 분야의 표준적 이론에 따르면, 혼잡의 외부비용만큼 혼잡통행료가 부과되고, 교통시설의 규모가 적정규모로 설정되는 경우, 징수된 통행료 수입은 일정한 조건하에서 교통시설의 소요 재원과 일치한다(이를테면 Small and Verhoef(2007) 참고). 즉 (1)교통량과 교통시설의 규모가 동일한 비율로 증가했을 때 혼잡비용이 불변이고, (2)교통시설 용량의 평균비용과 한계비용이 같으며, (3)교통혼잡과 교통시설 용량 등 두 측면에서 교통망이 최적화된 경우, 후생을 극대화하는 혼잡통행료(즉 최적 혼잡통행료)를 징수해 거두어들인 수입은 교통시설 운영에 필요한 재원을 과부족 없이 충당할 수 있다. 다시 말하면, 사회적 최적은 재정적 균형과 양립한다.
이러한 논의는 Mohring(1962)의 논의를 始發로 해, 도시경제학도의 연구에서도 언급되고 있다(Papageorgiou and Pines, 1999; Anas, 2012). 혼잡통행료의 부과 문제가 교과서적 이론에서 벗어나 현실도시에서 적용되고 있는 것이 최근의 추세이기 때문에, 혼잡통행료와 재원조달 문제, 그리고 교통시설의 최적 규모 문제를 통합해서 보는 문제는 더욱 중요한 정책적 관심사가 되고 있다. 이론적 관점에서 보아도 이 三者間 존재하는 상호의존성 때문에 혼잡통행료의 부과문제을 논하지 않고 교통시설 규모의 최적성과 투자문제를 논의할 수 없다.
그러나 최근의 문헌조사 논문(Lindsey, 2012)과 교재(Small and Verhoef, 2007)에도 잘 드러나 있는 것처럼, 교통망뿐 아니라 토지이용도 함께 고려한 공간모형을 이용해 자족성 원리를 검토한 연구는 아직 없다. 앞서 예시한 Papageorgiou and Pines(1999)의 경우 기본적으로 클럽이론(club theory)으로서 비공간모형에 속한다. Anas(2012)는 공간모형이지만 논문의 목적과 달리 중요 모형요소를 단순화함으로써 분석결과가 중대한 영향을 받게 되는데, 이러한 한계를 보정한 후 추가 연구가 수행될 필요가 있다.
교통현상은 일정 공간에 분포한 경제주체간 상호작용이 공간적으로 발현하는 현상이면서, 동시에 이러한 상호작용은 공간상 상호작용의 비용인 교통비용에 의해 영향을 받는다. 따라서 공간적 상호작용에 대해 가격을 설정하게 되는 혼잡통행료 역시 이러한 거시적 구조 속에서 분석할 필요가 있다. 이는 곧 분석방법론 측면에서 토지이용-교통모형을 이용해 혼잡통행료의 분석이 수행되어야 함을 의미한다.
혼잡통행료가 후생극대화적 관점에서 설정되어야 한다면, 이는 곧 토지이용-교통모형을 이용한 후생분석을 통해 책정되어야 함을 의미한다. 유상균⋅이혁주(2011)는 Anas and Kim(1996)류의 토지이용-교통모형에서 후생분석을 수행할 수 있는 방법론을 제시한다. 따라서 본 연구는 이들이 제시한 방법론을 적용해 혼잡통행료, 교통시설의 재원조달 및 교통시설의 최적규모 등 삼자간 관계에 대해 분석한다.
본 연구는 두 가지 점에서 기존 연구와 차이가 난다. 첫째, 토지시장 안에 내재된 교통망의 분석을 통해 자족성 원리를 검토한 논문은 아직 없는 것으로 파악된다. 본 연구는 교통망과 토지이용간 존재하는 상호작용을 定式分析할 수 있게 되는 토대가 될 것이다. 둘째, 유상균⋅이혁주(2011)의 방법론은 다양한 방면으로 확장되었다(이혁주, 2012, 2013 a,b). 그러나 이들 모형에서 교통시설은 암묵적으로 전제되었을 뿐 최적 교통시설과 관련된 논의는 없었다. 이러한 의미에서 본 논문은 기존의 유상균⋅이혁주(2011)가 제시한 방법론을 더욱 확장한다.
논문은 기존 문헌에 나타난 교통시설 재정적 자족성 원리에 대해 설명하는 것으로 시작된다. 이어서 일반균형 환경에서 토지이용-교통모형을 이용해 그 원리의 타당성을 확인한다. 먼저 교통시설을 도로면적으로 단순화한 후 자족성 원리를 확인한다. 교통시설의 투입요소로서 토지뿐 아니라 구조물과 같은 자본재를 도입하는 문제는 후속연구로 미룬다.
본 논문은 이론논문으로서 원리의 이해가 주요목적이기 때문에, 분석결과에 영향을 미치지 않는 모형 요소는 과감하게 단순화하고자 한다. 따라서 도시의 구역수를 2개로 단순화하고, 동일 구역에 속하는 토지는 주거와 생산 목적상 완벽하게 동질적(perfectly substitutable)이라고 가정한다. 교통비용 역시 교통시간으로 단순화되고 여타 부대 교통비용은 무시된다. 또한 통행은 통근통행만으로 구성된다고 가정된다. 뒤에서 확인이 가능하지만, 주요 공식이 교통량의 함수로 표현되는데, 이 교통량은 출퇴근 통행뿐 아니라 여타 통행을 포함하는 것으로 쉽게 확장되고, 논문의 결과에는 영향을 미치지 않는다.
II. 자족성의 원리
구역i의 통행비용을 통행량당gi, 교통량을Fi, 도로용량을Ri, 부과되는 통행료를ti라고 하자. 통행비용gi는 교통량Fi의 증가함수, 도로용량Ri의 감소함수로서gi≡g(FiRi)라고 쓰자. BPR (Bureau of Public Roads) 혼잡함수의 경우, 이 식은 보통

의 형태를 취한다(abc는 양의 상수).
한편 함수y=f(x1x2)가 어떤 상수α에 대해f(αx1αx2)일 때, 이 함수를 인수x1x2에 대해k차 동형이라고 말한다.k차 동형 함수의 경우, 오일러 정리에 따라

가 성립한다.
그런데 식(1)과 같은 혼잡함수의 경우, 교통량과 도로용량을 동일한 배율α로 증가시켰을 때, 혼잡함수의 값(즉 혼잡통행 비용)은 아무런 변화가 없다. 즉g(αFiαRi)=g(FiRi)=α0g(FiRi)으로서gi는 인수에 대해 0차 동형인 함수가 되고, 이는 식(2)에서k가 0이라는 뜻이다.

물론 이 식은 식(1)을 미분한 후 식(3) 좌변에 대입하여 그 값이 0이 됨을 직접 확인할 수도 있다.
구역 i 소재 토지의 기회비용을ri라고 하면, 최적 도로용량은 도로확장으로 인한 교통비용의 절약분 -Fi(∂gi/∂Ri)>0이 도로확장 비용ri와 일치할 때까지 확장되어야 한다. 즉 최적 도로용량Ri는

의 풀이가 된다. -∂gi/∂Ri>0는 도로용량을 1단위 늘릴 때 나타나는 통행비용 절약분을 말하고Fi는 도로 위의 교통량을 말하므로, 식(4)의 우변은 구역i를 통행하는 통행량 전체에서 실현되는 통행비용 절약분을 말한다.
한편 최적 혼잡통행료ti는 통행 1단위의 사회적 한계비용과 개인의 비용부담분gi간 차이

로 주어진다. 이 값은 물론 통행량 수준Fi에서 통행량 한 단위가 발생시키는 외부비용의 크기이다.
교통시설의 공급비용은 토지의 기회비용X도로면적=riRi이고, 교통부문의 수입은tiFi이므로, 도로부문의 재정수지 흑자는 재정수입 - 재정소요액인tiFi-riRi로 주어진다. 이 식을 식(4)-(5)를 이용해 다시 정리하자.

이 식에서 마지막 등호는 식(3)에 따른다. 즉 식(5)에 따라 최적의 혼잡통행료가 부과되고, 도로의 시설용량이 최적으로 선택되었을 때(즉 식(4)가 성립되도록 도로용량이 선택되었을 때), 도로 재정은 균형을 이루고 별도의 일반재원을 이용한 재정투입은 불필요하다.
식(6)은 임의의 구역[교통계획 용어로 링크(link) 혹은 아크(arc)]에서 성립하기 때문에, 교통망을 구성하는 각 링크에서 피구의 혼잡통행료가 부과되고 교통시설의 규모가 최적화되면, 자족성 원리는 전체 교통망에서 성립한다.
III. 모형
II절에서 보았던 것처럼 교통시설의 용량이 도로용량에 의해 전적으로 결정되는 경우, 식(6)과 같은 균형재정의 성립여부를 확인하고자 한다.
1. 모형의 구조
도시는 구역 1과 구역 2 두 개로 구성되어 있고, 구역 1은 도심, 구역 2는 외곽구역이라고 한다. 구역i에서 영업하는 X재 생산기업은 토지Qi, 노동Mi를 이용해 생산기술Xi=f(QiMi)에 따라 생산한다고 한다. 이 생산함수는 투입요소에 대해 1차 동형이라고 가정한다. X재의 단위 가격을pi, 노임이 시간당wi라고 하면, 이윤극대화 문제로부터

임을 알 수 있다. 생산함수의 양변을 전미분하면 dXi=(∂f/∂Mi)dMi+(∂f/∂Qi)dQi이고, 이 식의 양변에pi를 곱한 후, 식(7)을 이용해 결과식을

와 같이 정리할 수 있다.
생산함수가 투입요소에 대해 1차 동형이므로, 오일러 정리에 따라Xi=(∂f/∂Qi)Qi+(∂f/∂Mi)Mi이 성립한다. 이 식의 양변에 를 곱한 후, 식(7)을 이용해 정리하면 영이윤 방정식piXi=wiMi+riQi를 얻는다. 이 식의 양변을 전미분한 후, 식(8)을 이용해 정리하면 다음과 같은 식을 유도할 수 있다.

이 식은 뒤에 나오는 후생극대화 문제에서 이용된다.
이제 家口의 문제에 대해 알아보자. 구역i에 살면서 구역j로 출퇴근하는 어떤 가구를 가구 (ij)라고 부르자. 이 가구 (ij)는 X재(복합재)를xij만큼 자신의 거주구역인i에서 구매해 소비한다. 편의상 구매통행은 없는 것으로 한다. 또한 각 가구는 토지 면적qij와 여가시간lij를 소비한다. 이들 세 가지 재화를 소비함으로써 얻는 효용은 효용함수uij=u(xijqijlij)로 측정된다.
구역i를 1회 통행하는데 소요되는 시간을gi≡g(FiRi), 혼잡통행료를ti(#, 모수이거나 정책변수가 처음 나타날 때 # 표시), 구역 (ij)간 1회 통행시간을gij, 혼잡통행료를tij(#),라고 하자. 이때 g11=g1g22=g2g12=g21=g1+g2으로 정의된다.tij도 동일한 방식으로 정의하자. 각 가구는 단위 기간당 모두dij일 출근하고, 한번 출근해서 8시간(#)씩 일한다. 이때 단위기간당 총출퇴근 시간은gijdij이 되고, 혼잡통행료는 모두tijdij원 지출하게 된다.
가구당 총가용시간이H(#), 노동외 소득을D라고 하자. 이제 가구 (ij)의 소득 제약조건과 시간 제약조건을 다음과 같이 쓸 수 있다.

도시내 토지는N(#, 즉 폐쇄형 도시)명의 주민이 동일한 공유지분으로 소유한다. 노동외 소득은 지대수입과 혼잡통행료 환급금으로 구성된다.

이 식에서Ai(#)와Ri는 각각 구역i의 면적과 도로면적을 말하고, 도로면적은 교통시설의 규모를 대표하는 정책변수로서 계획가가 도시 주민의 후생을 극대화하도록 선택한다.
이상의 논의를 토대로 가구 (ij)의 효용극대화문제를 다음과 같이 쓸 수 있다.
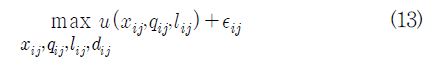
제약조건 식(10)-(12)
여기서εij(#)는 검불분포(Gumbel distribution)에 따르는 연속확률변수이다. 각 가구는 자신의 후생을 극대화하면서 노동외 소득, 교통시간, 통행료 등은 주어진 값으로 간주하고 극대화한다.
위 극대화 문제에 이용되는 라그랑지안은

와 같다. 이 식에서
 는 각각 소득 및 시간의 한계효용을 말한다. 효용극대화 문제를 푼 후, 간접효용함수Vij를 구할 수 있다. 검불분포를 이용해 특정 가구가 구역짝 (ij)를 최선의 주거-직장짝으로 선택할 확률Pij를 이 간접효용함수를 이용해 표현할 수 있다. 그리고 시스템의 전반적 후생수준을W는 최대효용의 기대치인
는 각각 소득 및 시간의 한계효용을 말한다. 효용극대화 문제를 푼 후, 간접효용함수Vij를 구할 수 있다. 검불분포를 이용해 특정 가구가 구역짝 (ij)를 최선의 주거-직장짝으로 선택할 확률Pij를 이 간접효용함수를 이용해 표현할 수 있다. 그리고 시스템의 전반적 후생수준을W는 최대효용의 기대치인

로 정의하자. 여기서 λ(#)는 확률변수∈ij의 분산과 밀접하게 관련된 검불 확률분포의 母數이다.
이제 시장균형 조건을 나열하면 다음과 같다.

여기에 영이윤조건 2개를 더해 모두 8개의 방정식이 존재한다. 미지수는 가격변수{ripiwi}2i=16개와, X재 생산량X1X22개 등 모두 8개이다. 이들 8개 변수를 앞으로 ‘기본변수’라고 부르자. 방정식의 수가 기본변수의 수와 똑같으므로, 기본변수를 위 시장균형 조건을 이용해 유도할 수 있다. 여타 내생변수는 모두 이들 변수의 함수로 주어진다.
그런데 효용극대화 문제로부터 간접효용함수Vij를, (1)기본변수 8개 가운데r1r2piwj등 4개의 미지수와 (2)내생변수인 교통량F1F2및 (3)정책변수인 통행료와 도로용량의 함수로 표현할 수 있음을 알 수 있다. 따라서 간접효용함수Vij를

와 같이 정책변수는 생략하고 내생변수만 이용해 쓰자. 다만 또 다른 내생변수인F1F2는 생략했다. 이 두 내생변수는 앞서 본 8개 기본변수 모두의 함수이다. 이 생략문제는 뒤에서 다시 설명한다.
2. 후생함수의 변화율
후생함수W의 정책변수에 대한 변화율을 차례대로 구하자. 정책변수t1t2R1R2에 따라 특정 균형이 달성되고 이 균형상태에 대응하는 기본변수의 값이 결정된다. 그리고 이 기본변수의 값에 따라 후생함수W의 값이 결정된다. 따라서W를W(t1t2R1R2)라고 쓸 수 있다.

위 식에서 간접효용함수의 변화율을 구하기 전에 간접효용함수에 포함된 노동외 소득D의 변화율부터 구하면 편리하다.

tk가 변하면 기본변수 모두가 변하고, 이들 모든 변화는 교통량Fi의 변화를 유발할 것이다. 식(14) 의 교통량 변화율은 이들 모든 변화를 한꺼번에 잡아내고 있다. 따라서 식(11)을 기술하면서 내생변수Fi를 생략하고 간접효용함수를 표현했지만, 결국 식(14)를 통해 정책변수가 교통량Fn에 미치는 모든 일반균형적 (직간접) 영향이dFn/dtk식을 통해 한꺼번에 잡혔다.
이제 식(13)-(14)를 이용해 혼잡통행료에 대한 간접효용함수의 변화율을 구하자. 그 값은 기본적으로 이혁주(2012)에 잘 나와 있으므로 그 결과를 차용하자.

이제Rk도로면적 에 대한 후생함수W의 변화율을 구하자. 이 변화율은 식(12)와 유사하게

로 주어진다.
그런데 이혁주(2012) 및 관련연구(이혁주, 2013a, b)에서 수차례 나타난 것처럼, 식(16) 우변 첫 세 항의 값은 근사적으로 0으로 주어진다. 따라서

로 주어진다. 이 식에서 간접효용함수의 도로면적에 대한 변화율은 다음과 같이 계산된다.

이 식에서wij는 기종점이 (ij)이 통행자(즉 주거지가 구역i, 직장소재지가 구역j인 어떤 가구)의 시간의 기회비용을 말한다(이 점은 효용극대화 문제를 이용해 보일 수 있다).
식(18)을 식(17)에 대입하고 정리하자.

식(19)의 마지막 항을 유도하는 과정은 이혁주(2012) 식(17)에 나타나 있다.
그런데g≡g(FiRi)이고, 어떤 구역의 도로면적Rk가 변하면 이에 따라 도시 전역 각 구역의 교통량Fi도 변하므로 전미분dgi/dRk는 다음과 같이 계산된다.

이 식에서δik는 두 아래 첨자가 동일구역을 말할 때는 1, 나머지 경우는 0의 값을 취하는 함수이다. 식(20)을 식(19) 우변 두 번째 항에 대입하자.

식(21)을 식(19)에 대입한 후 정리하면 다음과 같은 결과를 얻는다.

이 식에서 전미분 기호dgi/dRk와 편미분 기호∂gi/∂Rk는 엄격히 구분해 사용했다.
IV. 논의
혼잡 통행료와 도로재정간 관계를 규명하기 전에 유상균⋅이혁주(2011)의 방법론이 토지시장 속에 내재된 교통망의 분석방법론으로서 어떤 의미를 가지는지 먼저 명확히 하자.
1. 표준방법론 비판
본 연구에서 특정 기종점간 교통수요는 교통량Fij로서Fij는Fij=NPijdij로 표현된다. 그런데 출퇴근일수dij는 효용극대화 문제의 풀이로 주어지는 마샬의 수요함수로서, 가구가 푸는 여느 내생변수xijqijlij와 조금도 다르지 않게 母數인 소득, 시장에서 주어지는 각종 가격, 혼잡통행료와 도로면적 등 정책변수 등의 함수로 표현된다. 따라서 이들 모수가 변하면 수요함수xijqijlij가 이동(shift)하듯이 교통수요 함수Fij=NPijdij도 고정되어 있지 않고 이동하게 된다.
이렇게 교통수요 함수를 각종 모수의 함수로 전제하는 것은 교통망 분석의 표준적 방식과 분명히 다른 점이다. 즉 표준 교통망 모형에서 교통수요함수는 정책변수에 대해 이동이 허용되지 않는 고정된 함수로 취급되고, 이러한 가정하에서 식(4)-(5)가 유도되며, 이렇게 유도된 식(4)-(5)를 이용해 식(6)의 자족성이 성립하는 것으로 분석한다. 예컨대 교통경제학 교과서로서 널리 알려진 Small and Verhoef(2007), 자족성 원리를 일정한 기술적 조건하에서 정리한 Yang and Meng(2002)를 참조하여 알아보면 다음과 같다.
교통망 분석에서 사회적 후생함수를 본 논문에서 이용하는 간접효용함수의 기호V를 이용해 나타내고, 교통수요함수를F(.)(좀 더 정확히 표현하면 교통에 대한 역수요함수)f를 교통량이라고 하자.

제약조건은 수요곡선의 높이F(f)가 총통행비용g(.)+t와 일치할 때 교통시장은 균형에 이른다는 사실을 보이는 식이다. 사회적 후생V는 교통수요곡선F(.) 아래에 있는 면적(즉 교통수요의 실현에서 통행자가 얻어가는 총편익의 크기)에서 교통비용f(.)(즉 문헌에서 말하는 이용자 비용인 user cost)과 교통시설 비용rR=도로의 단위면적당 취득비용도로면적 등을 뺀 금액이 된다.
먼저 최적 혼잡통행료t의 식을 유도해 보자. 쿤-터커 조건을 이용해 미분하는 것도 가능하지만, 제약조건을 나중에 반영하기로 하고 목적함수부터 미분하면 다음과 같다.

그런데 시장균형 조건F(f)=g(tR)+t으로부터F(f)-g(tR)=t이므로 이 결과를 이용해 위 식을 다시 정리하면 다음과 같다.

표준 교통망 분석에서는 식(24)의 첫 항을 0으로 놓는다. 이는

으로 놓는다는 의미이고, 교통수요 함수F(.)가 정책변수인t를 因數로 포함하지 않는다는 뜻이다. 그러나 교통수요함수를 효용함수와 같이 통행자의 효용극대화 문제의 풀이를 통해 構成하는 경우, 마샬의 수요함수에 불과한 교통수요 함수F(.)는 소비자 효용극대화 문제의 母數인 정책변수t를 당연히 포함해야 한다. 이때 식(25)는 성립하지 않는다.
만약 교통수요 함수F(.)가 정책변수t를 포함하는 경우∂F(n)/∂t는 더 이상 0이 아니고, 표준모형이 말하는 바와 같이 최적 혼잡통행료 또한 식(24)의 마지막 항만을 0으로 하는t=f[∂g/∂t]로 주어지리라는 보장이 없다. 또한∂F(n)/∂t는 더 이상 0이 아니기 때문에 식(24)를 푸는 최적 혼잡통행료는 교통망 분석의 표준적 방법론을 이용해서는 더 이상 구할 수도 없게 된다. 정책변수R에 대해서도 똑 같이 설명할 수 있다.
환언하면, 저자가 아는 바로는 기존의 표준적 교통망 분석기법을 이용하게 되면 일반적 형태의 교통수요 함수를 전제로 한 교통망 분석은 불가능하다. 본 논문은 유상균⋅이혁주(2011)의 방법론을 이용해 표준적 방법론의 한계를 극복한다.
2. 혼잡통행료와 도로재정
후생을 극대화하는 최적 혼잡통행료와 최적 도로용량은 식(15)와 식(22)를 동시에 만족시키는 풀이로 주어진다. 즉 다음과 같은 수식을 유도할 수 있다.

이들 두 식은 비록 식(25)와 같은 가정을 동원해 유도한 교통망 분석의 표준모형과 분석방법론을 이용해 유도한 결과와 일치한다. 이때 도로부문의 재정흑자는 각 구역에서tiFi-riRi로 주어지는데, 그 규모를 식(26)을 이용해 따져보면 다음과 같다.

식(3)을 이용하면 위 식 마지막 괄호는 0이 된다. 즉 식(26)하에서 도로재정은 균형을 이룬다.
이 분석결과는 비록 식(25)가 성립하지 않는 보다 일반적인 상황에서도 표준모형이 이야기하는 자족성의 원리가 성립한다는 의미이다.
V. 결론
본 연구는 기존 연구에 비해 현저하게 확장된 환경에서 교통시설의 자족성 원리가 표준적 조건하에서 성립됨을 보여준다. 이러한 의미에서 이 자족성 원리는 일반성이 큰 원리라고 말할 수 있다.
본 연구가 제시하는 관점에서 교통망을 토지시장 속에 포함시키는 분석은 향후 더 진행되어야 한다. 이러한 본격적 분석에 앞서 두 가지 선행연구가 필요해 보인다.
첫째, 유상균⋅이혁주(2011)의 분석방법론은 도시의 반경이 가변적인 경우에도 적용할 수 있는 방법론이다. 이를 교통망 분석적 관점에서 재해석하면, 교통망을 구성하는 각 링크의 크기가 변하고 결절점(node)의 수도 증가 혹은 감소하는 교통망 분석에도 이들이 제안한 방법론을 적용할 수 있다는 말이다. 교통망 분석 표준모형에서는 교통망의 물리적 규모는 고정되어 있는 것으로 가정된다. 이 가정은 본 논문에서도 이용한 설정방식이었다. 그러나 이와 달리 교통망 규모 자체가 가변적인 경우, 이를테면 市域 자체가 변해 교통망 자체가 변해야 하는 경우, 과연 자족성의 원리가 여전히 성립하는지 추가 확인이 필요하다. 유상균⋅이혁주(2011) 방법론이 시사하는 바에 따르면, 이를테면 혼잡통행료 부과로 市域이 축소되면 이로 인해 교통망 건설⋅유지비용이 절약되고, 이러한 편익은 최적 혼잡통행료 설계에 반영되어야 한다. 이때 식(26)에 따라 주어지는 표준적인 피구조세는 더 이상 최적이 아니다. 이때 식(28)과 달리 자족성의 원리가 성립하지 않을 수 있게 된다. 이러한 분석 역시 표준적인 방법론을 이용해 규명할 수는 없는 문제로서, 유상균⋅이혁주(2011)의 방법론을 적용하여 규명해야 한다.
둘째, 본 연구는 도로교통 서비스의 생산에 필요한 투입요소로서 도로면적만을 가정하고 논의를 진행했다. 교통시설의 투입요소를 좀 더 다양화한 후 자족성의 원리가 여전히 성립하는지 추가 규명이 필요하다.
셋째, 본 연구에서 다룬 家口는 異質的이다. 이질적 경제주체의 경우 별도의 특별한 분석적 조치를 취하지 않는 한, 개별 주체의 효용을 합쳐 사회적 후생함수를 구성하는 과정에서(즉 선형 혹은 비선형 변환을 통해 사회적 후생함수의 구성하는 과정에서) 불가피하게 ‘종합화의 문제’(aggregation problem)이 발생한다. 이 경우 결정모형(deterministic model)과 달리 후생함수의 1계 도함수는 소득의 한계효용과 소비자 후생변화분간 共分散 項을 포함하게 되고, 표준논의와 상당히 다른 분석적 결과가 초래된다. 이 문제는 교통 및 도시경제학분야에서 그 잠재적 중요성에도 불구하고 본격적으로 논의되고 있지 않은데, 본 연구모형을 이용해 그 분석적 시사가 더 연구되어야 할 것으로 보인다.
References
-
유상균, 이혁주, (2011), “수치해석적 공간균형모형의 후생함수에 대한 연구와 시사”, 「국토계획」, 46(4), p199-208.
Yu, Sanggyun, and Rhee, Hyok-Joo, (2011), "A Study of the Welfare Function of a Spatial Equilibrium Model and the Implications", Journal of Korea Planners Association, 46(4), p199-208. -
이혁주, (2012), "토지이용-교통 일반균형 모형의 후생함수와 혼잡통행료", 「국토계획」, 47(4), p183-192.
Rhee, Hyok-Joo, (2012), "Welfare Function of Theory-Based Spatial Equilibrium Models and Congestion Tolls", Journal of Korea Planners Association, 47(4), p183-192. -
이혁주, (2013a), "집적의 경제가 구현된 공간균형모형의 분석방법론", 「국토계획」, 48(1), p181-189.
Rhee, Hyok-Joo., (2013a), "Analytical Metho- dology of the Spatial Equilibrium Model with Agglomeration Economies", Journal of Korea Planners Association, 48(1), p181-189. -
이혁주, (2013b), “조세가 이미 존재하는 정책환경에서 혼잡통행료의 일반균형적 분석방법론”, 「국토계획」, 48(3), p293-306.
Rhee, Hyok-Joo, (2013b), "General Equilibrium Analysis of Congestion Tolls in the Presence of Distortinary Taxes: A Methodology", Journal of Korea Planners Association, 48(3), p293-306. - Anas, Alex, (2012), "The Optimal Pricing, Finance and Supply of Urban Transportation in General Equilibrium: A Theoretical Exposi- tion.", Economics of Transportation, 1, p64-73.
-
Anas, Alex, and Kim, Ikki, (1996), “General Equilibrium Models of Polycentric Urban Land Use with Endogenous Congestion and Job Agglomeration”, Journal of Urban Economics, 40, p232-256.
[https://doi.org/10.1006/juec.1996.0031]

- Harberger, Arnold C., (1971), "Three Basic Postulates for Applied Welfare Economics: An Interpretive Essay", Journal of Economic Literature, 9, p785-797.
-
Lindsey, Robin, (2012), "Road Pricing and Investment", Economics of Transportation, 1, p49-63.
[https://doi.org/10.1016/j.ecotra.2012.07.001]

- Mohring, Herbert, (1962), Highway Benefits, Northwestern University Press.
-
Papageorgiou, Yorgos Y., and Pines, David, (1999), , An Essay on Urban Economic Theory, Norwell, Massachusetts: Kluwer Academic Publishers..
[https://doi.org/10.1007/978-1-4615-4947-5]

-
Samuelson, Paul A, (1954), "The Pure Theory of Public Expenditure", Review of Economics and Statistics, 36, p387-389.
[https://doi.org/10.2307/1925895]

- Small, Kenneth, Verhoef, Erik, (2007), , The Economics of Urban Transportation, New York: Routledge.
-
Yang, H., and Meng, Q., (2002), "A Note 'Highway Pricing and Capacity Choice in a Road Network under a Build-Operate -Transfer Scheme'", Transportation Research Part A, 36, p659-663.
[https://doi.org/10.1016/S0191-2615(01)00018-2]
